Question

A solid cylinder made of wax is of base radius 6 cm and height 12 cm. A cone of the same radius and height is carved out from this.
(a) What is the volume of this cone?
(b) How many candles of cylindrical shape of 1 cm radius and 12 cm height can be made with the remaining wax?

Answer 1

Hint: To calculate the volume of the cone, use the formula \[\dfrac{\pi {{r}^{2}}h}{3}\], where r is the radius of the cone and h is the height of the cone. To count the number of candles that can be made from the remaining wax, calculate the volume of the solid cylinder using the formula \[\pi {{r}^{2}}h\]. Subtract the volume of the cone from the volume of the cylinder to get the volume of the remaining wax. Divide the volume of the remaining wax by the volume of the cylindrical candle to calculate the number of candles that can be carved out.

Complete step-by-step solution -
We have data regarding a cone of radius 6cm and height 12cm. We also have data about cylindrical candles of radius 1cm and height 12cm.
(a) We have to calculate the volume of the cone which has radius 6cm and height 12cm.
We know that the volume of the cone is \[\dfrac{\pi {{r}^{2}}h}{3}\], where r is the radius of the cone and h is the the height of the cone.
  

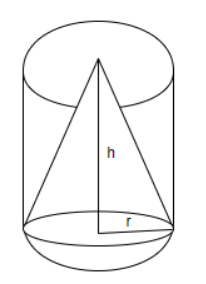
Substituting \[r=6cm,h=12cm\] in the above equation, the volume of the cone \[=\dfrac{\pi {{r}^{2}}h}{3}=\dfrac{3.14{{\left( 6 \right)}^{2}}\left( 12 \right)}{3}=452.16c{{m}^{3}}\].
Hence, the volume of the cone carved out of the cylinder with radius 6cm and height 12cm is \[452.16c{{m}^{3}}\].
(b) We have to calculate the number of cylindrical candles that can be made from the remaining wax.
We will calculate the volume of the cylinder with radius 6cm and height 12cm.
We know the volume of the cylinder with radius r and height h is given by \[\pi {{r}^{2}}h\].
Substituting \[r=6cm,h=12cm\] in the above formula, the volume of the the cylinder \[=\pi {{r}^{2}}h=\left( 3.14 \right){{\left( 6 \right)}^{2}}\left( 12 \right)=1356.48c{{m}^{3}}\].
Thus, the volume of the solid cylinder is \[1356.48c{{m}^{3}}\].
We know that the volume of the cone is \[452.16c{{m}^{3}}\].
The remaining volume of wax can be obtained by subtracting the volume of the cone from the volume of the cylinder.
Thus, the remaining volume \[=1356.48c{{m}^{3}}-452.16c{{m}^{3}}=904.32c{{m}^{3}}\].
We will now calculate the number of cylindrical candles which can be made from the remaining wax.
We will calculate the volume of each cylindrical candle. We know that the candle has radius 1cm and height 12cm.

 

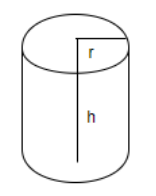
We know that the volume of the cylinder with radius r and height h is given by \[\pi {{r}^{2}}h\].
Substituting \[r=1cm,h=12cm\] in the above formula, the volume of the cylinder \[=\pi {{r}^{2}}h=3.14{{\left( 1 \right)}^{2}}\left( 12 \right)=37.68c{{m}^{3}}\].
Thus, the volume of each cylindrical candle is \[37.68c{{m}^{3}}\].
To calculate the number of candles that can be made out of the remaining wax, we will divide the volume of cones by the volume of the remaining wax.
Thus, the number of cones \[=\dfrac{904.32}{37.68}=24\].
Hence, 24 cylindrical candles can be made out of the remaining wax.

Note: One must be extremely careful about units while calculating the volume of the cone and the cylinder. Length of any object is given in centimetres. So, the volume will be calculated in cubic centimetres. Also, one must observe that the number of candles is a dimensionless quantity.