Question

A solid cylinder and a hollow cylinder, both of the same mass and same external diameter are released from the same height at the same time on an inclined plane. Both roll down without slipping, which one will reach the bottom first?
A. Both together only when angle of incidence of plane is $45^{\circ}$
B. Both together
C. Hollow cylinder
D. Solid cylinder

Answer 1

Hint: We will first find out the moment of inertia of both the cylinders and then will use the formula of acceleration of an object rolling down an inclined plane without slipping. Then by using the equations of motions, we can find the time for both the cylinders.
Formula used: $a=\dfrac{gsin\theta}{1+\dfrac{I}{MR^2}}$

Complete step by step answer:

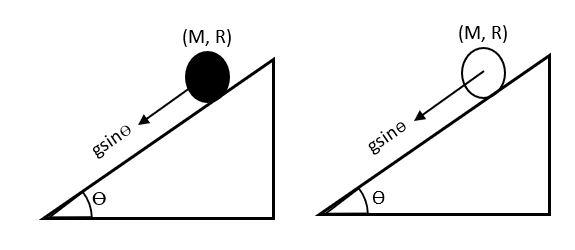
Let us assume the mass of both solid and hollow cylinder by M and their radius be R, both rolling down an inclined plane of length $l$ making angle $\theta$ with the horizontal without slipping.

We know that, acceleration of a purely rolling object along an inclined plane without slipping is given by, $a=\dfrac{gsin\theta}{1+\dfrac{I}{MR^2}}$ ………. (i)
where, $\theta$ is the inclination of the plane, I is the moment of inertia of the object about an axis perpendicular to its cross-section, M is the mass of the object and R is its equivalent radius.
Now, as per the question both cylinders were released from rest. So, using the distance formula from the equations of motion, we get $S=\dfrac{1}{2}at^2$
As the length of inclined plane is $l$ and putting the value of acceleration from equation (i), we get $S=\dfrac{1}{2}\times \left(\dfrac{gsin\theta}{1+\dfrac{I}{MR^2}}\right)t^2$
$\implies t=\sqrt{2l\left(\dfrac{1+\dfrac{I}{MR^2}}{gsin\theta}\right)}$ ………. (ii)

For solid cylinder,
Moment of inertia, ${I}_{s} = \dfrac{MR^2}{2}$
Therefore, time taken by the solid cylinder to reach the bottom of incline using equation (ii),
${t}_{s}=\sqrt{2l\left(\dfrac{1+\dfrac{MR^2 /2}{MR^2}}{gsin\theta}\right)}=\sqrt{\dfrac{3l}{gsin\theta}}$ ………. (iii)
Now, for hollow cylinder,
Moment of inertia, ${I}_{h} = MR^2$
Therefore, time taken by the solid cylinder to reach the bottom of incline using equation (ii),
${t}_{h} =\sqrt{2l\left(\dfrac{1+\dfrac{MR^2}{MR^2}}{gsin\theta}\right)}=\sqrt{\dfrac{4l}{gsin\theta}}$ ………. (iv)
So, clearly from the equations (iii) and (iv), we can say that ${t}_{s}<{t}_{h}$.
Thus, the solid cylinder will reach the bottom first. Hence, the correct answer is option D.

Note:
The formula for time that we derived can also be used directly. But for concept clearance, we derived here the formula. We can also use the conservation of energy at the point of release and at the bottom to find the final velocity of the cylinders, which in turn can give the time required.