Question

A solid cone of radius $r$ and height $h$ is placed over a solid cylinder having the same base radius and height as that of a cone. The total surface area of a combined solid is:
(A) $\pi r\left[ \sqrt{{{r}^{2}}+{{h}^{2}}}+3r+2h \right]$
(B) $\pi r\left[ \sqrt{{{r}^{2}}+{{h}^{2}}}+2r+3h \right]$
(C) $\pi r\left[ 2\sqrt{{{r}^{2}}+{{h}^{2}}}+3r+2h \right]$
(D) None of these

Answer 1

Hint: For answering this question we will have to use the basic mensuration formulae. The curved surface area of a cylinder is given as $2\pi rh$. The curved surface area of a cone is given as $\pi rl=\pi r\sqrt{{{r}^{2}}+{{h}^{2}}}$ . The base area of the cylinder that is the area of the circle is given by $\pi {{r}^{2}}$. And then apply them and derive the total surface area of the combined solid.

Complete step-by-step solution
Now considering the question we have a solid cone of radius $r$ and height $h$ which is placed over a solid cylinder having the same base radius and height as that of the cone. We need to find the total surface area of the combined solid.

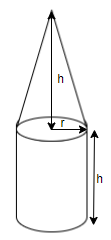
We can say that the total surface area of the combined solid will be equal to the sum of the curved surface area of a cone and the curved surface area of the cylinder and base area.
Mathematically expressed as, $\text{the total surface area= C}\text{.S}\text{.A of cone+C}\text{.S}\text{.A of cylinder+base area}$ .
From the basic concept, we know that the curved surface area of a cylinder is given as $2\pi rh$. The curved surface area of a cone is given as $\pi rl=\pi r\sqrt{{{r}^{2}}+{{h}^{2}}}$ . The base area of the cylinder that is the area of the circle is given by $\pi {{r}^{2}}$.
So the total surface area of the combined solid will be equal to $\pi r\sqrt{{{r}^{2}}+{{h}^{2}}}+2\pi rh+\pi {{r}^{2}}=\pi r\left[ \sqrt{{{r}^{2}}+{{h}^{2}}}+2h+r \right]$ .
Hence we can conclude that the total surface area of a solid formed by placing a solid cone of radius $r$ and height $h$ placed over a solid cylinder having the same base radius and height as that of a cone is given by $\pi r\left[ \sqrt{{{r}^{2}}+{{h}^{2}}}+2h+r \right]$.
Hence, option D is the correct answer and marks it because any of the other options are not correct.

Note: While answering this question we will have to be sure with the calculations and formulae. If we made a mistake and write a formula wrong then we will end up having a wrong answer like we had written the base area as $3\pi {{r}^{2}}$. We will have the final answer as $\pi r\left[ \sqrt{{{r}^{2}}+{{h}^{2}}}+2h+3r \right]$ . So we will mark option A which is wrong.