Question

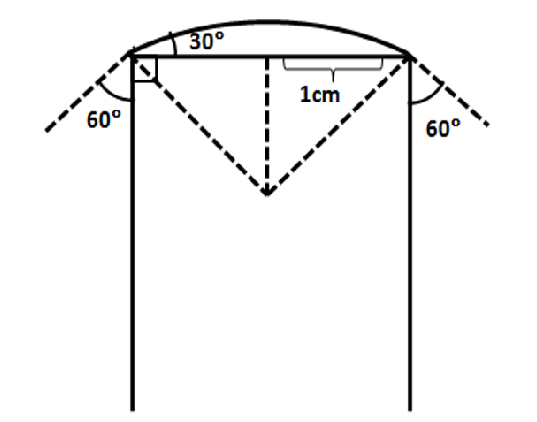
A soap bubble is being blown on a tube of radius\[1cm\]. The surface tension of the soap solution is \[0.05N/m\] and the bubble makes an angle of \[{60^ \circ }\]with the tube as shown. The excess of pressure over the atmospheric pressure in the tube is:

A. \[5Pa\]
B. \[1Pa\]
C. \[10Pa\]
D. \[20Pa\]

Answer 1

Hint:The bubble is making an angle of \[{60^ \circ }\]with the tube. Therefore, the bubble is bulged outside and appears to be convex upwards. There will be an atmospheric pressure on the bubble due to the weight of the air in the atmosphere. Also, there will be excess pressure acting downwards as a resultant of surface tension that can be calculated by the resultant force of surface tension.

Formula Used: The excess of pressure inside the tube is given as: \[p = \dfrac{{2T}}{R}\] where, \[T\] is the surface tension acting on the surface of the bubble

\[R\] is the resultant of the surface tension directed inside the bubble.

Complete step by step solution:
The surface tension acts along the free surface of the liquid. So, if the
The surface of liquid is convex upwards as shown in the diagram, the resultant of the surface tension acting along the tangent at the location of the molecule is directed into the liquid. Due to this inward force, the Pressure inside the liquid is higher than that outside it.

Therefore, the excess of pressure inside the soap bubble or in the tube is given as
\[p = \dfrac{{2T}}{R}\]\[ \to (1)\]
where, \[T\] is the surface tension acting on the surface of the bubble
\[R\]is the resultant of the surface tension directed inside the bubble.

It is given that the tube has a radius = \[r = 1cm = 0.01m\], and
the surface tension of the soap solution = \[T = 0.05N/m\]

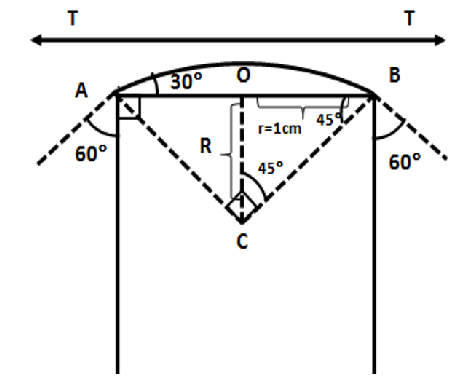
Also, it is given in the diagram that the soap bubble makes an angle of \[{60^ \circ }\]with the vertical surface and \[{30^ \circ }\] with the horizontal surface of the tube. Drawing lines \[AC\] and \[BC\] such that \[\angle ACB = {90^ \circ }\]

Therefore, \[\angle OCB = {45^ \circ }\]

In \[\Delta OBC\], \[\operatorname{ta} {45^ \circ } = \dfrac{r}{R} \to R = \dfrac{r}{{\tan {{45}^ \circ
}}}\]

Substituting in equation (1)
\[p = \dfrac{{2T}}{{\left( {\dfrac{r}{{\tan {{45}^ \circ }}}} \right)}} = \dfrac{{2T}}{{\left( {\dfrac{r}{1}}
\right)}} = \dfrac{{2T}}{r}\]

Substituting the values
\[p = \dfrac{{2T}}{r} = \dfrac{{2 \times 0.05}}{{0.01}} = 10Pa\]
Thus, the excess of pressure over the atmospheric pressure in the tube is \[5Pa\].

Hence, option (A) is the correct answer.

Note: The excess pressure depends on the shape of the liquid surface and the resultant of surface tension. In case of liquid surface that is convex upwards, the pressure inside the liquid is higher than outside it (assuming that the pressure outside the liquid is atmospheric pressure). And, in case of liquid surface that is concave upwards, the pressure inside the liquid is less than outside.