Question

A smooth sphere of radius R is made to translate in a line with a constant acceleration $a=g$. A particle kept on the top of the sphere is released from there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a function of the angle $\theta$ as it slides down.
A.$\sqrt{Rg(1+sin\theta-cos\theta)}$
B.$\sqrt{2Rg(2+sin\theta-cos\theta)}$
C.$\sqrt{2Rg(1+sin\theta-cos\theta)}$
D.$\sqrt{2Rg(1-sin\theta-cos\theta)}$

Answer 1

Hint: A good way to go about solving this problem is to assume applicability of the work-energy theorem to this situation. Consider an angular displacement of the particle. First find the magnitude of the gravitational and pseudo forces acting on the particle. Note that the pseudo force on the particle arises from the acceleration of the sphere. Then find the net work done by all forces in the system, which will be equivalent to the change in kinetic energy of the particle due to its motion under the influence of the pseudo force, following which you should consequently arrive at the appropriate velocity relation.

Formula Used:
Work energy theorem: $W_{net} = \Delta KE$

Complete answer:
A smooth sphere implies there are no frictional forces at play, and the translational acceleration of the sphere is constant and equivalent to the magnitude of the acceleration due to gravity g.
The particle of mass m experiences two forces owing to its state of motion over the sphere. It experiences a gravitational force acting vertically downwards, and a pseudo force acting towards the right, since we assume that the motion of the sphere is towards the left.
The gravitational force acting on the particle is given as $F_{g} = mg$,
And the pseudo force acting on the particle is given as $F_{f} = ma$

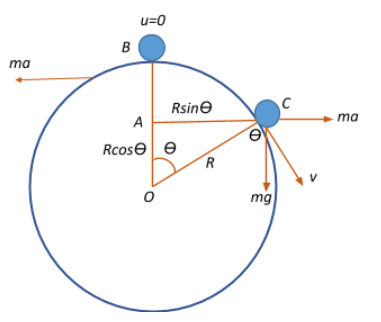
From the work energy theorem which states that the net work done by the forces on an object equals the change in its kinetic energy, we have the work done by the gravitational and the pseudo forces to be $W_{g}$ and $W_{f}$ respectively given by:
$W_{g} + W_{f} = \Delta KE$
The work done by the gravitational force is given as:
$W_{g} = F_{g}(AB) = mg(OB-OA) = mg(R-Rcos\theta) = mgR(1-cos\theta))$, where $\theta$ is the angular displacement of the particle and R is the radius of the sphere.
The work done by the pseudo force is given as:
$W_{f} = F_{f}(AC) = ma(Rsin\theta)$
The change in kinetic energy for this particle comes only from the motion of the particle under the influence of the pseudo force, i.e., $\Delta KE = \Delta KE_{f} = KE_{f}$ since initially it possesses no velocity.
$\Rightarrow \Delta KE = KE_f = \dfrac{1}{2}mv^2$
Now, applying all these relations into our work energy theorem expression:
$W_{g} + W_{f} = \Delta KE$
$\Rightarrow mgR(1-cos\theta) + ma(Rsin\theta) = \dfrac{1}{2}mv^2$
Given in the question that $a=g$:
$\Rightarrow mgR(1-cos\theta) + mgR(sin\theta) = \dfrac{1}{2}mv^2$
$\Rightarrow mgR(1-cos\theta + sin\theta) = \dfrac{1}{2}mv^2$
$\Rightarrow v^2 = 2gR(1+sin\theta-cos\theta)$
$\Rightarrow v = \sqrt{2gR(1+sin\theta-cos\theta)}$

Note:
Note that we consider the change in kinetic energy of the particle as the kinetic energy arising from the influence of just the pseudo force and not the gravitational force since the kinematic motion of the particle is brought about by the pseudo acceleration of the particle sliding down arising from the acceleration of the sphere in the opposite direction.
Also, remember to be cautious while using directionally resolved components and consider only those that are actually influencing direction-specific motion of any object.