Question

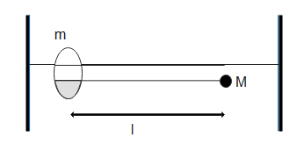
A smooth ring of mass \[m\] which is free to slide along a rigid horizontal wire, is connected to a particle of mass $M$ by a string of length $l$. The system is released from rest when the string is horizontal. At an instant when string becomes vertical, the speed of the particle

A. $0$
B. $\sqrt {2gl\dfrac{{(m + M)}}{m}} $
C. $m\sqrt {\dfrac{{2gl}}{{M(m + M)}}} $
D. $m\sqrt {\dfrac{{2gl}}{{m(m + M)}}} $

Answer 1

Hint: We are given a ring that is free to slide along a rigid horizontal wire and it is connected to a particle of mass and then the system is released when the string is horizontal and we need to find the speed of the particle when the string becomes vertical.

Complete step by step answer:
We know that the momentum of the ring and the particle connected to it will be equal
$mv = MV$
Where $v$ and $V$ are the velocities of the ring and the particle respectively.
Hence $u = \dfrac{{MV}}{m}$ where $u$ is the initial velocity of the ring when the string is released. Now the potential energy of the string will get converted into the kinetic energy of the ring as well as the particle therefore we have,
$Mgl = \dfrac{1}{2}m{u^2} + \dfrac{1}{2}M{V^2}$
Substituting the value of the initial velocity of the ring we get
$ \Rightarrow 2Mgl = m{\left( {\dfrac{{MV}}{m}} \right)^2} + M{V^2}$
Further solving we get,
$ \Rightarrow 2Mgl = m\dfrac{{{M^2}{V^2}}}{{{m^2}}} + M{V^2}$
$ \Rightarrow 2gl = \dfrac{{M{V^2}}}{m} + {V^2}$
Rearranging the equation to get the desired expression for the speed of the particle
$ \Rightarrow 2gl = \dfrac{{(M + m)}}{m}{V^2}$
$ \Rightarrow V = \sqrt {\dfrac{{2mgl}}{{M + m}}} $
$\therefore V = m\sqrt {\dfrac{{2gl}}{{m(M + m)}}} $

Hence option D is the correct answer.

Note: The ring is attached to the horizontal wire and it can freely move only in the forwarding and backwards direction while the mass attached to the string can move in the upward and downward direction. So when the string is released the mass will move in the downward direction due to gravity and the string will become vertical. In the horizontal direction, there is no external force applied and therefore the momentum of the ring and the particle is conserved and that is why we equated them at the beginning of the solution.