Question

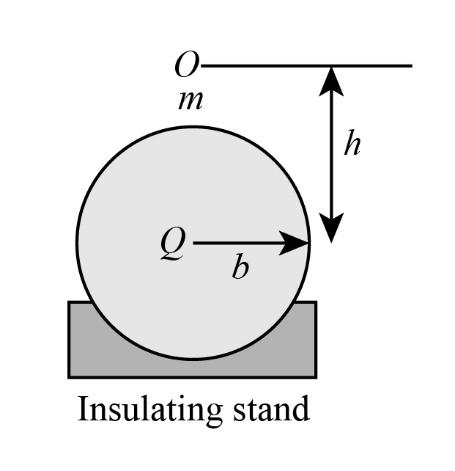
When a small uncharged conducting ball of radius \[a = 1{\rm{ cm}}\] and mass \[m = 50{\rm{ g}}\] is dropped from a height h above the centre of another large conducting sphere of radius b\[\left( { = 1{\rm{ m}}} \right)\] having charge Q\[\left( {100{\rm{ }}\mu {\rm{C}}} \right)\], it rises to a height \[{h_1}\]\[\left( { = 2{\rm{ m}}} \right)\] after the collision. The value of h is \[\dfrac{x}{{10}}\]. Find x.
Assume that during the impact there is no dissipation of energy.

Answer 1

Hint: We will be using the concept of conservation of energy of the small ball and sphere system, which says that the summation of total energy before the collision is equal to the summation of total energy after the collision.

Complete step by step answer:
Given:
The radius of the small uncharged conducting ball is \[a = 1{\rm{ cm}} = 1{\rm{ cm}} \times \left( {\dfrac{{\rm{m}}}{{100{\rm{ cm}}}}} \right) = 0.01{\rm{ m}}\].
The mass of the small uncharged conducting ball is \[m = 50{\rm{ g}} = 50{\rm{ g}} \times \dfrac{{{\rm{kg}}}}{{1000{\rm{ g}}}} = 0.05{\rm{ kg}}\].
The radius of the large conducting sphere is \[b = 1{\rm{ m}}\].
The charge on the large sphere is \[Q = 100{\rm{ }}\mu {\rm{C}}\].
The large sphere rises to height after the collision is \[{h_1} = 2{\rm{ m}}\].
The value of height h is equal to \[\dfrac{x}{{10}}\].

We have to find the value of x.

Let us write the expression for the potential energy of the large sphere.
\[P = \dfrac{{kQ}}{b}\]
Here, k is a constant, and its value is given by
\[k = \dfrac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}{\rm{ N}}{{\rm{m}}^2}{{\rm{C}}^{ - 2}}\]
Here \[{\varepsilon _0}\] is the permittivity of free space or permittivity of vacuum.

Similarly, we can write the expression for the potential of the small sphere.
\[P' = \dfrac{{kq}}{a}\]

We are given that a small ball is colliding with a large sphere that means are coming into contact with each other, and we know that the potential energy of two bodies at the same energy levels is equal so we can equate the potential of a small ball and large sphere as below:
\[\dfrac{{kQ}}{b} = \dfrac{{kq}}{a}\]
We will rearrange the above expression to get the value of the charge of a small ball.
\[q = \dfrac{{Qa}}{b}\]

On substituting \[100{\rm{ }}\mu {\rm{C}}\] for Q, \[1{\rm{ cm}}\] for a and \[1{\rm{ m}}\] for b in the above expression, we get:
\[\begin{array}{c}
q = \dfrac{{\left( {100{\rm{ }}\mu {\rm{C}}} \right)\left( {0.01{\rm{ m}}} \right)}}{{\left( {1{\rm{ m}}} \right)}}\\
 = 1{\rm{ }}\mu {\rm{C}}
\end{array}\]

Let us write the expression for conservation of energy given by the system's total energy before collision equal to total energy after the collision.
\[\dfrac{1}{2}m{\left( {\sqrt {2gh} } \right)^2} + \dfrac{{kqQ}}{b} = mg{h_1} + \dfrac{{kqQ}}{{b + {h_1}}}\]
Here g is the acceleration due to gravity, and its value is \[9.8{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}\].
On rearranging the above expression, we get:
\[\begin{array}{l}
\dfrac{1}{2}m{\left( {\sqrt {2gh} } \right)^2} + \dfrac{{kqQ}}{b} = mg{h_1} + \dfrac{{kqQ}}{{b + {h_1}}}\\
\dfrac{1}{2}mg\left( {2h - {h_1}} \right) = kqQ\left( {\dfrac{1}{{b + {h_1}}} - \dfrac{1}{b}} \right)
\end{array}\]
On substituting \[0.05{\rm{ kg}}\] for m, \[2{\rm{ m}}\] for \[{h_1}\], \[9.8{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}\] for g, \[0.01{\rm{ m}}\] for a, \[1{\rm{ m}}\] for b, \[100{\rm{ }}\mu {\rm{C}}\] for Q and \[1{\rm{ }}\mu {\rm{C}}\] for q in the above expression, we get:
$
\dfrac{1}{2}\left( {0.05{\rm{ kg}}} \right)\left( {9.8{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}} \right)\left( {2h - 2{\rm{ m}}} \right) = \left( {9 \times {{10}^9}{\rm{ N}}{{\rm{m}}^2}{{\rm{C}}^{ - 2}}} \right)\left( {1{\rm{ }}\mu {\rm{C}}} \right)\left( {100{\rm{ }}\mu {\rm{C}}} \right)\left( {\dfrac{1}{{1{\rm{ m}} + 2{\rm{ m}}}} - \dfrac{1}{{1{\rm{ m}}}}} \right)\theta \\
0.245{\rm{ }}{{{\rm{kg}} \cdot {\rm{m}}} {\left/
 {\vphantom {{{\rm{kg}} \cdot {\rm{m}}} {{{\rm{s}}^2} \times \left( {\dfrac{{\rm{N}}}{{{{{\rm{kg}} \cdot {\rm{m}}} {\left/
 {\vphantom {{{\rm{kg}} \cdot {\rm{m}}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}}}} \right)}}} \right.
 } {{{\rm{s}}^2} \times \left( {\dfrac{{\rm{N}}}{{{{{\rm{kg}} \cdot {\rm{m}}} {\left/
 {\vphantom {{{\rm{kg}} \cdot {\rm{m}}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}}}} \right)}}\left( {2h - 2{\rm{ m}}} \right) = 9 \times {10^9}{\rm{ N}}{{\rm{m}}^2}\left( {100 \times {{10}^{ - 12}}} \right)\left( { - 0.66} \right)\\ $
$\implies h = 0.8{\rm{ m}}$

On substituting \[\dfrac{x}{{10}}\] for h in the above expression, we get:
\[\begin{array}{c}
\dfrac{x}{{10}} = 0.8{\rm{ m}}\\
x = 8{\rm{ m}}
\end{array}\]

Therefore, the value of x is \[8{\rm{ m}}\].

Note:
We can remember the conversion of Newton into its base units (kg, m, s) so that the law of homogeneity of units can be followed. Do not forget to substitute \[{10^{ - 6}}\] for micro in the final expression of energy conservation.