Question

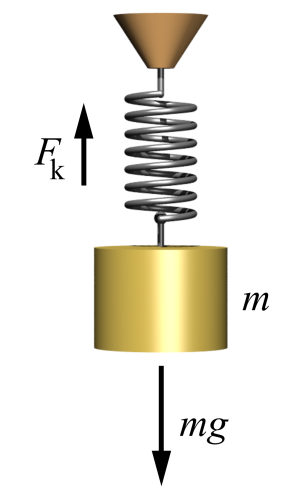
A small boy attached to one end of a vertically hanging spring is performing SHM about its mean position with the angular frequency $\omega$ and amplitude \[\text{a}\]. If at height y from the mean position the body gets detached from the spring. Calculate the value of \[y\] so that the height obtained by the mass is maximum. The body does not interact with the spring during its subsequent motion after detachment.

Answer 1

Hint: A vertical spring-mass system will undergo simple harmonic motion in the vertical direction about the equilibrium position, the force (F) needed to extend or compress a spring by some distance. $h=y+\dfrac{(\omega\sqrt {(a^{2}-y^{2})^{2}}}{{2g}}$

Formula used: $h=y+\dfrac{(\omega\sqrt {(a^{2}-y^{2})^{2}}}{{2g}}$

Complete step-by-step solution -
A vertical spring-mass system will undergo simple harmonic motion in the vertical direction about the equilibrium position. The motion will be centered about a point of equilibrium where the net force on the mass is zero rather than where the spring is at its rest position. If the mass is displaced from the equilibrium position, the spring exerts a restoring elastic force that obeys Hooke's law, which states that, the force (F) needed to extend or compress a spring is directly proportional to the distance $x$.
Mathematically, the restoring force F is given by $F=-kx$ where $k$ is spring constant and $x$ is displacement from the equilibrium.
We know that the height is given by:$h=y+\dfrac{v^{2}}{2g}$ where y is height from the mean position the body gets detached from the spring, $v$ is the velocity under SHM
Also $v=\omega\sqrt{( a^{2}-y^{2})}$ where a is amplitude and $\omega$ is angular frequency.
then$h=y+\dfrac{(\omega\sqrt {(a^{2}-y^{2})^{2}}}{{2g}}$
for h to be max,$\dfrac{dh}{dy}=0$
$\dfrac{dh}{dy}=1+\dfrac{\omega^{2}}{2g}(-2y)=0$
$1-\dfrac{\omega^{2}}{2g}(2y)=0$
$y=\dfrac{g}{\omega^{2}}$
Hence $y=\dfrac{g}{\omega^{2}}$ for maximum height.

Additional Information:
Simple harmonic motion is a special type of periodic motion where the restoring force on the moving object is directly proportional to the object's displacement magnitude and acts towards the object's equilibrium position. It results in an oscillation which, if uninhibited by friction or any other dissipation of energy, continues indefinitely. The following physical systems are some examples of simple harmonic oscillators: mass on a spring, uniform circular motion, mass on a simple pendulum.

Note: A vertical spring-mass system will undergo simple harmonic motion, about the mean position The force (F) needed to extend or compress a spring is given by $F=-kx$ where –ve imples against the force.