Question

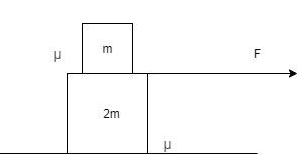
A small box of mass $m$ is placed on a top of a larger box of mass $2m$ as shown in the diagram. When a force $F$ is applied to the large box, both boxes accelerate to the right with the same acceleration. If the coefficient of friction between all surfaces is $\mu $ what would be the force accelerating the smaller mass?

A) $\dfrac{F}{3} - mg\mu $
B) $F - 3mg\mu $
C) $F - mg\mu $
D) $\dfrac{{F - mg\mu }}{3}$

Answer 1

Hint:When a force is applied on a system, it attains an acceleration. The friction generally prevents the motion of the object on the surface. The friction occurs opposite to the motion. The friction solely acts on the surfaces and hence against the reaction force exerted on the body from the ground.

Complete step by step answer:
Formulae Used:
If an object of mass $m$ is moving on a surface with a coefficient of friction $\mu $, then the applied frictional force on the object acting opposite to the direction of the motion of the object is
${F_f} = \mu N$
where, $N$ is the normal reaction force on the object by the surface which on a flat surface is equal to the vertically downward acting gravitational force $mg$, where $g$ is the acceleration due to gravity.
$\therefore {F_f} = \mu mg$
Given:
The small box has a mass of $m$.
The larger box on which the small box is placed has a mass of $2m$.
The applied force on the large box is $F$.
Both the boxes acquire the same acceleration due to the force.
The coefficient of friction between all the surfaces is $\mu $.
To get: The force producing acceleration on the smaller box.
Step 1:
Both the boxes have the same acceleration, so effectively you can consider the two boxes to be a system of mass $\left( {m + 2m} \right)$ with an acceleration of say $a$.
So calculate the effective frictional force on the system by the ground surface
${F_f} = \mu \left( {m + 2m} \right)g = 3\mu mg$
Step 2:
So, the effective force acting on the system is
$
  F - {F_f} \\
   \Rightarrow F - 3\mu mg \\
 $
Now this force effectively produces the acceleration on the whole system.
So, you can write
$
  {F_{effective}} = 3ma \\
   \Rightarrow F - 3\mu mg = 3ma \\
   \Rightarrow \dfrac{F}{{3m}} - \mu g = a \\
 $
So you get the effective acceleration of the system as $a = \dfrac{F}{{3m}} - \mu g$
Step 3:
The smaller block of mass $m$ acquires the same acceleration $a$ and hence the force producing the acceleration on the body is
$
  {F_{smaller}} = ma \\
   \Rightarrow {F_{smaller}} = m \times \left( {\dfrac{F}{{3m}} - \mu g} \right) \\
   \Rightarrow {F_{smaller}} = \dfrac{F}{3} - \mu mg \\
 $
$\therefore $ you found the force, producing acceleration on the smaller box as $\dfrac{F}{3} - \mu mg$ .

Final Answer:The force accelerating the smaller mass is (A) $\dfrac{F}{3} - mg\mu $.

Note:The effective force acting on the system of the body will be affected only by the friction at the surface of the ground. You can see that the surface between the smaller box and the larger box will have no roe there as this is playing within the system. You can also consider the frictions separately. For that, you have to consider the effective forces on each of the masses and equate the acceleration. This process will lead you eventually to the same answer.