Question

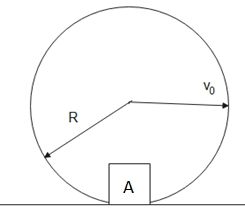
A small body A is fixed to the inside of a thin rigid hoop of radius \[R\] and mass equal to that of A. The hoop rolls without slipping over a horizontal plane; at the moments when body A gets into lower position, the centre of the hoop moves with velocity \[{{v}_{0}}\]. At what values for \[{{v}_{0}}\] will the hoop move without bouncing?
 

Answer 1

Hint: When block A is at the topmost point of the hoop, the normal force acting on the hoop will be in the upwards direction and therefore the possibility for it to bounce will be maximum at that point. At that point, the velocity of the hoop will decrease considerably, so using conservation of mechanical energy we can solve equations to find the value of \[{{v}_{0}}\].

Formulas used:
\[\omega =\dfrac{v}{R}\]
\[K=\dfrac{1}{2}I{{\omega }^{2}}\]
\[K=\dfrac{1}{2}m{{v}^{2}}\]

Complete step by step solution:
Let the velocity of the point of hoop in contact with the ground be \[{{v}_{r}}\]
For condition of rolling without slipping-
\[{{v}_{r}}={{v}_{0}}\] -------- (1)
We know that,
\[{{v}_{r}}=\omega r\] --------- (2)
Here,
\[\omega \]is the angular velocity of the hoop
\[r\]is distance from the axis of rotation, \[\therefore r=R\]
 From eq (1) and eq (2), we get,
\[\omega =\dfrac{{{v}_{0}}}{R}\] -------- (3)
For the hoop to move without bouncing, the maximum chances of it to bounce will be when block A will be at the topmost point of the hoop, at point M. At this point, let velocity of hoop be \[v\]
 

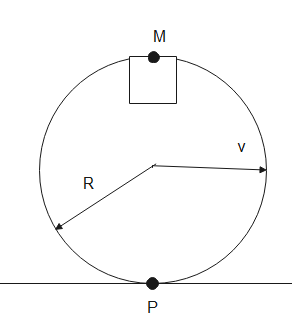
Initial kinetic energy of the system of loop will be-
\[{{K}_{i}}=\dfrac{1}{2}{{I}_{P}}{{\omega }^{2}}\]
Here,\[{{I}_{P}}\] is the moment of inertia of the hoop about point P.
\[{{K}_{i}}=\dfrac{1}{2}[m{{R}^{2}}+m{{R}^{2}}]{{\left( \dfrac{{{v}_{0}}}{R} \right)}^{2}}\] (Moment of inertia of block A will be zero about point P)
\[\Rightarrow {{K}_{i}}=m{{v}_{0}}^{2}\] ------- (4)
Kinetic energy of the hoop system when block A is on point P
\[{{K}_{f}}=\dfrac{1}{2}[m{{(2R)}^{2}}+m{{R}^{2}}+m{{R}^{2}}]{{\left( \dfrac{v}{R} \right)}^{2}}\]
 \[{{K}_{f}}=3m{{v}^{2}}\] ---------- (5)
Since no external forces are acting on the body, the total mechanical energy of the system is conserved.
\[mgR+{{K}_{i}}=[mg(2R)+mgR]+{{K}_{f}}\]
Here \[mgR\] and \[3mgR\] are potential energies of the hoop system at point P and M respectively.
Substituting values from eq (4) and eq (5) in the above eq, we get,
\[m{{v}_{0}}^{2}-3m{{v}^{2}}=2mgR\] ------- (6)

 The centripetal force will be provided by the net force acting on the system. Therefore,
\[\begin{align}
  & 2mg-N=mR{{\omega }^{2}} \\
 & \Rightarrow 2mg-N=mR{{\left( \dfrac{v}{R} \right)}^{2}} \\
 & \Rightarrow (2mg-N)R=m{{v}^{2}} \\
 & \therefore \left( \dfrac{2mg-N}{m} \right)R={{v}^{2}} \\
\end{align}\]
Here,\[N\]is the normal force acting between ground and hoop
Substituting the value of \[{{v}^{2}}\] In eq (6),
\[m{{v}_{0}}^{2}-3(2mg-N)R=2mgR\]
For the condition for hoop to roll without bouncing, \[{{N}_{A}}=0\](\[{{N}_{A}}\] is normal force acting on hoop due to block A. As \[N={{N}_{A}}=0\], from the above eq,
\[\begin{align}
  & m{{v}_{0}}^{2}=8mgR \\
 & \therefore {{v}_{0}}=\sqrt{8gR} \\
\end{align}\]
Therefore, for \[{{v}_{0}}=\sqrt{8gR}\] the hoop and block system will roll without bouncing.

Note:
The velocity of centre of mass of the system will be \[{{v}_{0}}\]. As the block moves from point P to point M, its potential energy increases and kinetic energy decreases due to which the energy of the system also decreases. This process continues as the system keeps rolling. For an isolated system, the mechanical energy and momentum are conserved.