Question

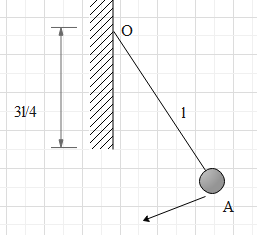
A small bob attached to a light inextensible thread of length $l$ has a periodic time when allowed to vibrate as a simple pendulum. The thread is now suspended from a fixed end of a vertical rigid rod of length $\dfrac{{3l}}{4}$ (as shown in the figure). Find the periodic time if the pendulum performs periodic oscillations in this arrangement.

Answer 1

Hint: Time period of a simple pendulum is given by the equation $T = 2\pi \sqrt {\dfrac{l}{g}} $ .Towards the right side of mean position, it oscillates with length $l$and towards the left side of mean position length is reduced to $\dfrac{l}{4}$.

Complete step by step answer:
Time period of a simple pendulum is given by the equation $T = 2\pi \sqrt {\dfrac{l}{g}} $
Step 1:
Towards the right side of the mean position, it oscillates with length $l$ but towards the left side of the mean, position length is reduced due to the obstruction created by the rod. Since the length of the rod is $\dfrac{{3l}}{4}$, the length of the pendulum on the left side of the mean position is given by $l - \dfrac{{3l}}{4}$.
Step 2:
The time period of the right side can be written as ${T_R} = \dfrac{1}{2}\left( {2\pi \sqrt {\dfrac{l}{g}} } \right)$ and time period for left side can be written as ,
$
\Rightarrow {T_L} = \dfrac{1}{2}\left( {2\pi \sqrt {\dfrac{{\left( {l - \dfrac{{3l}}{4}} \right)}}{g}} } \right) \\
\Rightarrow {T_L} = \dfrac{1}{2}\left( {2\pi \sqrt {\dfrac{{\left( {\dfrac{l}{4}} \right)}}{g}} } \right) \\
 $
Step 3
Total time period is given by the sum of time periods of left and right sides of the oscillation. Therefore ,Time period ,
${T_{new}} = {T_R} + {T_L}$
Substituting the values found in step 2 into the equation, we get
\[
\Rightarrow {T_{new}} = \dfrac{1}{2}\left( {2\pi \sqrt {\dfrac{l}{g}} } \right) + \dfrac{1}{2}\left( {2\pi \sqrt {\dfrac{{\left( {\dfrac{l}{4}} \right)}}{g}} } \right) \\
\Rightarrow {T_{new}} = \dfrac{1}{2}\left( {2\pi \sqrt {\dfrac{l}{g}} } \right) + \dfrac{1}{2}\left( {\dfrac{1}{2}2\pi \sqrt {\dfrac{l}{g}} } \right) \\
\Rightarrow {T_{new}} = \dfrac{1}{2}T + \dfrac{1}{4}T \\
\Rightarrow {T_{new}} = \dfrac{3}{4}T \\
 \]

Note:
While taking the time period of the oscillation on the left and right side, make sure we take half the time period for that particular length. Because $T = 2\pi \sqrt {\dfrac{l}{g}} $ gives the time period of one full oscillation of length $l$ but we are getting only half oscillation for both the lengths.so we should take half the time periods of corresponding lengths.