Question

A small block of mass m kept at the left end of a larger block of mass\[M\]and length\[~L\]. The system can slide on a horizontal road. The system is started towards right with an initial velocity v. The friction coefficient between the road and the bigger block is$\mu $ and that between the block is\[~\dfrac{\mu }{2}\]. Find the time elapsed before the smaller blocks separates from the bigger block.

Answer 1

Hint: While solving this problem first consider the small block then calculate acceleration and friction force, then similarly for the bigger block. Since friction is acted by the road, use the formula of friction force. Then take whole bodies as one system, calculate net acceleration. Now to calculate the time elapsed, use the kinematic equation.
Formula used:
Formula of friction force is given by,
$f=\mu N$
Where,
$\begin{align}
  & f=\text{friction force} \\
 & \mu \text{= friction coefficient} \\
 & \text{N=normal force} \\
\end{align}$
Formula of Kinematic equation is given by,
$x=vt+\dfrac{1}{2}at$
Where,
  $\begin{align}
  & x=\text{ displacement} \\
 & v=\text{velocity} \\
 & t=\text{time} \\
 & a=\text{ acceleration} \\
\end{align}$

Complete step by step answer:

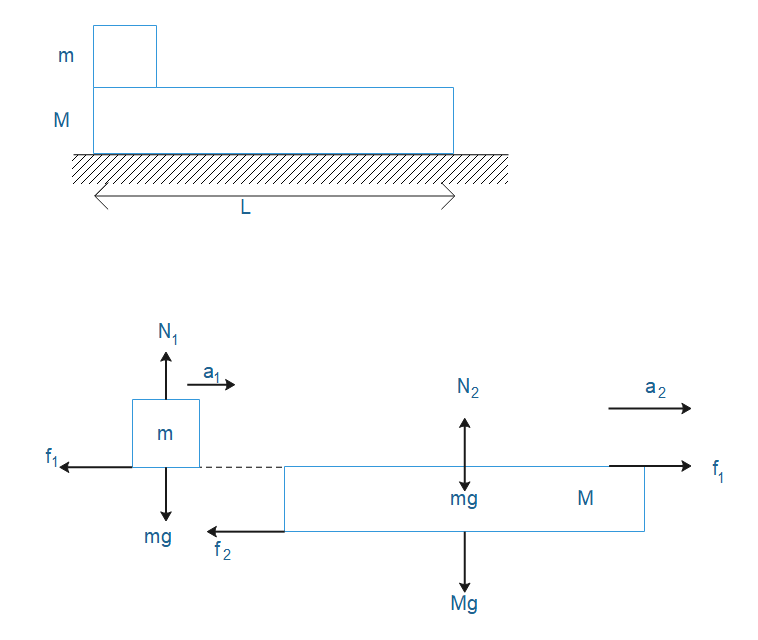
A small block is placed on the bigger block which slips on the bigger block to fall from the rear end. As seen from the road, both the blocks are moving towards right, of course the velocity of the bigger block is smaller than that of the larger block.
The mass of the small box is $m$and the mass of the bigger block is$M$. Length of bigger block is$L$.
As it is given that initial velocity is$v$.
The friction coefficient between blocks (bigger and smaller) is ${{\mu }_{1}}=\dfrac{\mu }{2}$ and friction coefficient between road and larger block is${{\mu }_{2}}=\mu $.
Consider the free body diagram of blocks which is shown below where we have resolved the force acting on the block.
Let, the acceleration of a small block is${{a}_{1}}$. The acceleration of the larger block is${{a}_{2}}$.
Now we will calculate friction force between blocks which is given by,
$\begin{align}
  & {{f}_{1}}={{\mu }_{1}}{{N}_{1}} \\
 & {{f}_{1}}=\dfrac{\mu }{2}\left( mg \right) \\
 & {{f}_{1}}=\dfrac{\mu mg}{2} \\
\end{align}$
Now let’s calculate acceleration of small block which is given by,
$\begin{align}
  & -{{f}_{1}}=m{{a}_{1}} \\
 & -\dfrac{\mu mg}{2}=m{{a}_{1}} \\
 & {{a}_{1}}=-\dfrac{\mu g}{2} \\
\end{align}$
Now we will calculate friction force between road and larger block which is given by,
\[\begin{align}
  & {{f}_{2}}={{\mu }_{2}}{{N}_{2}} \\
 & {{f}_{2}}=\mu (mg+Mg) \\
 & {{f}_{2}}=\mu (m+M)g \\
\end{align}\]
We have already calculate acceleration of small block, now we need to calculate acceleration of bigger block which is given by,
\[\begin{align}
  & {{f}_{1}}-{{f}_{2}}=M{{a}_{2}} \\
 & \dfrac{\mu mg}{2}-\mu (m+M)g=m{{a}_{2}} \\
 & -\dfrac{\mu mg}{2}-\mu Mg=m{{a}_{2}} \\
\end{align}\]
\[\begin{align}
  & {{a}_{2}}=\dfrac{-\mu mg-2\mu Mg}{2M} \\
 & {{a}_{2}}=\dfrac{-\mu g}{2}\left( \dfrac{m+2M}{M} \right) \\
\end{align}\]
Now if we consider both the block as one system then the net acceleration of the system is given by,
\[\begin{align}
  & {{a}_{1}}-{{a}_{2}}=\left( -\dfrac{\mu g}{2} \right)-\dfrac{-\mu g}{2}\left( \dfrac{m+2M}{M} \right) \\
 & {{a}_{1}}-{{a}_{2}}=\left( -\dfrac{\mu g}{2} \right)+\dfrac{\mu g}{2}\left( \dfrac{m+2M}{M} \right) \\
 & {{a}_{1}}-{{a}_{2}}=\left( \dfrac{\mu g}{2} \right)\left( -1+\dfrac{m+2M}{M} \right) \\
 & {{a}_{1}}-{{a}_{2}}=\mu g\left( \dfrac{m+M}{2M} \right)---(1) \\
\end{align}\]
The distance travel by small and bigger block in time $t$is given by,
${{x}_{m}}=vt+\dfrac{1}{2}{{a}_{1}}{{t}^{2}}\text{ and }{{x}_{M}}=vt+\dfrac{1}{2}{{a}_{2}}{{t}^{2}}$
Now if we consider separate point of block, then total length is given by,
${{x}_{M}}+L={{x}_{m}}$
$\begin{align}
  & vt+\dfrac{1}{2}{{a}_{1}}{{t}^{2}}=vt+\dfrac{1}{2}{{a}_{2}}{{t}^{2}}+L \\
 & \dfrac{1}{2}{{a}_{1}}{{t}^{2}}-\dfrac{1}{2}{{a}_{2}}{{t}^{2}}+L \\
 & t=\sqrt{\dfrac{2L}{{{a}_{1}}-{{a}_{2}}}} \\
\end{align}$
Put value from equation one in above equation,
 $t=\sqrt{\dfrac{2L}{\dfrac{\mu g(m+M)}{2M}}}=\sqrt{\dfrac{4M}{\mu g(m+M)}}$
Therefore the time elapsed before the smaller blocks separate from the bigger block is given by$\sqrt{\dfrac{4M}{\mu g(m+M)}}$

Note: When two solid bodies slip over each other, the force of friction is called kinetic friction. If two bodies don't slip on each other then the force of friction is called static friction. The friction force on an object is acted in the opposite direction of the motion of that particular object. It can be calculated by multiplying the normal reaction i.e.$N$ between object and surface with the friction coefficient between them. Do prefer kinematic equations, when there is a need to calculate time, velocity and etc. The perpendicular component of kinetic friction is called the normal contact force or normal force and the parallel component of kinetic friction is called friction.