Question

A small block of mass m is kept on a rough inclined surface of inclination \[\theta \] fixed in an elevator. The elevator goes up with a uniform velocity v and the block does not slide on the wedge. The work done by the force of friction on the block in time t will be
A. Zero
B. \[mgvt{\cos ^2}\theta \]
C. \[mgvt{\sin ^2}\theta \]
D. \[mgvt{\sin 2}\theta \]

Answer 1

Hint: First of all, draw the diagram of moving elevator with uniform velocity v. Then calculate the displacement made by the block and then find the work done by friction by using the work done formula.

Complete step-by-step solution -
Formulae used: \[W = \vec f.\vec d\cos \alpha \]
Given mass of block = m
Surface of inclination = \[\theta \]
Uniform velocity of the elevator going upwards = v
The figure for the moving elevator is given by:

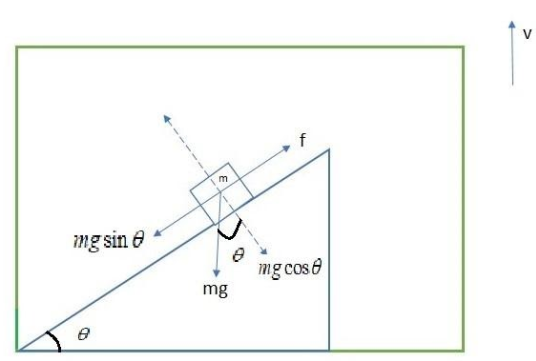
Here,
Displacement of block in time \[t\] is given by \[d = vt\]
We know that work done by friction \[ = {\text{force of friction }}{\text{. displacement }}\cos \alpha \]
i.e., \[W = \vec f.\vec d\cos \alpha \]
from the figure it is clear that,
\[ \Rightarrow \vec f = mg\sin \theta \\
   \Rightarrow \vec d = vt \\
   \Rightarrow \alpha = {90^0} - \theta \\ \]
Where \[\alpha \] is the angle of between force and displacement
So, work done by the force of the friction on the block in time \[t\] is given by
\[ \Rightarrow W = mg\sin \theta .\left( {vt} \right)\cos \left( {{{90}^0} - \theta } \right) \\
   \Rightarrow W = mgvt\sin \theta \sin \theta \\
  \therefore W = mgvt{\sin ^2}\theta \\ \]
Thus, the correct option is C. \[mgvt{\sin ^2}\theta \].

Note: The frictional force, \[f\] of the inclined plane on the load acts parallel to the surface, and is always in a direction opposite to the motion of the object. In the given problem the mass of the object acts downwards w.r.t gravitational force equals to \[mg\].