Question

A small beam of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring rotates freely about its center o. The bead comes to rest relative to the ring. Then, the final angular velocity of the system,
A. $v/R$
B. $2v/R$
C. $v/2R$
D. $3v/R$

Answer 1

Hint:First, we should use the equation of linear angular momentum of the system, ${L_i} = mvR$to calculate the initial angular velocity of the system and $I = m{R^2}$ to calculate the inertia of the system. Then calculate the final angular momentum as ${L_f} = I\omega $ and put it in $I = m{R^2}$. Then, apply the law of conservation of angular momentum to calculate final angular momentum

Complete step by step solution:

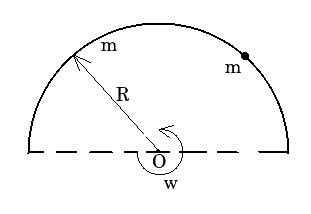
Given,
The velocity of the small beam is $v{\rm{ }}$
The mass of the small beam is $m$
The radius of the ring is $R$
The initial angular velocity is ${\omega _i} = 0\,$.
The final angular velocity is ${\omega _f}$.
The equation of initial angular momentum of the beam of mass$m$ and velocity $v{\rm{ }}$moving in a circular ring of radius $R$can be written as,
${L_i} = mvR$ …… (1)
The net inertia of the system can be written as,
${I_{system}} = {I_{bead}} + {I_{ring}}$ …… (2)
The inertia of the bead and ring can be written as,
${I_{bead}} = {I_{ring}} = m{R^2}$ …… (3)
Substituting equation (3) in equation (2) we get,
${I_{system}} = m{R^2} + m{R^2} = 2m{R^2}$ …… (4)
Again, we have,
${L_f} = {I_{system}}{\omega _f}$ …… (5)
Applying law of conservation of angular momentum, we have,
${L_i} = {L_f}$ …… (6)
Substituting equation (1) in equation (6) and equation (5) in equation (6) we have,
$mvR = {I_{system}}{\omega _f}$ …… (7)
Substituting value of ${I_{system}}$from equation (4) in equation (7) we get,
$\begin{array}{l}mvR = (2m{R^2}){\omega _f}\\ \Rightarrow {\omega _f} = \dfrac{v}{{2R}}\end{array}$

Hence, the correct answer is (C).

Note: The beam moves with a linear velocity $v{\rm{ }}$ and its angular velocity is zero. The ring rotates with angular velocity \[{\omega _f}\]. In the solution, the students can use the law of conservation of angular momentum where the initial momentum is equal to the final momentum.