Question

A small bead of mass \[M\] slides on a smooth wire that is bent in a circle of radius \[R\] . It is released at the top of the circular part of the wire (point \[A\] in the figure) with a negligible small velocity. Find the height \[H\] where the bead will reverse direction:

A. \[R\]
B. \[2R\]
C. \[\dfrac{{3R}}{2}\]
D. \[\dfrac{{5R}}{2}\]

Answer 1

Hint: In this problem, we have to use the concept of conservation of energy of a body. It is inevitable that energy at initial position will be equal to the energy at final position. A body when placed at a certain height just starts to move contains both the potential energy and the kinetic energy.

Formula used:
The potential energy of a body is given as:
\[P.E = mgh\]
Where,
\[m\] indicates the mass of the body.
\[g\] indicates the acceleration due to gravity.
\[h\] indicates the position of the body from the ground level.
The kinetic energy of a body is given by:
\[K.E = \dfrac{1}{2}m{v^2}\]
Where,
\[m\] indicates the mass of the body.
\[v\] indicates the velocity at which the body is moving.

Complete step by step answer:
In the given question, we are supplied with the following data:
There is a small bead of mass \[M\] slides on a smooth wire that is bent in a circle.The radius of the circle is given as \[R\] .The bead is released at the top of the circular part of the wire (point \[A\] in the figure) with a negligible small velocity. We are asked to find the height where the bead will reverse its direction of motion.

To begin with, we will draw the diagram with other dimensions added, for the better understanding.

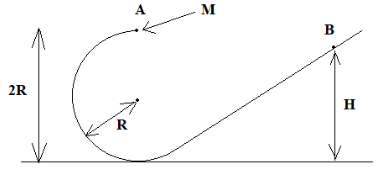
From the diagram, it can be seen that the height of the bead initially was \[2R\] from the ground, which is the diameter of the circle. At the point \[A\] , the velocity is zero.
Total energy of the bead at the point \[A\] is given as:
\[{E_{\text{A}}} = mg \times 2R + \dfrac{1}{2} \times m \times {0^2}\] …… (1)

At the point \[B\] , the velocity is also zero.
Total energy of the bead at the point \[B\] is given as:
\[{E_{\text{B}}} = mg \times H + \dfrac{1}{2} \times m \times {0^2}\] …… (2)
Now, we will equate both the equations (1) and (2):
$mg \times 2R + \dfrac{1}{2} \times m \times {0^2} = mg \times H + \dfrac{1}{2} \times m \times {0^2} \\
\Rightarrow mg \times 2R = mg \times H \\
\therefore H = 2R$
Hence, the height where the bead will reverse its direction of motion is \[2R\] .

The correct option is B.

Note: While solving this problem, it is important to remember that at the \[B\] , the bead reverses its direction. It is because the initial energy of the bead is equal to the energy of the bead at the point \[B\] . It is important to remember that the velocity at these two points is zero. Velocity at the point \[B\] becomes zero, as the bead ceases to move forward any further.