Question

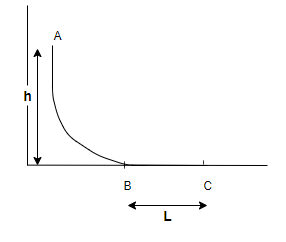
A small ball of mass m starts at a point A with speed \[{v_0}\]​ and moves along a frictionless track AB as shown. The track BC has coefficient of friction \[\mu \]. The ball comes to stop at C after travelling a distance \[L\]. Find \[L\].

                                          

(A) \[\dfrac{{2h}}{\mu } + \dfrac{{\mathop v\nolimits_0^2 }}{{2\mu g}}\]
(B) \[\dfrac{h}{\mu } + \dfrac{{\mathop v\nolimits_0^2 }}{{2\mu g}}\]
(C) \[\dfrac{h}{{2\mu }} + \dfrac{{\mathop v\nolimits_0^2 }}{{\mu g}}\]
(D) \[\dfrac{{4h}}{\mu } + \dfrac{{\mathop v\nolimits_0^2 }}{{2\mu g}}\]

Answer 1

Hint: The given problem is an example of motion of a particle in frictionless and frictional track. As in this problem the particle is at some height \[h\] and then starts moving along the given track from A to C and stops at C. So, this problem can be solved using the law of energy conservation.

Step-by-step solution:
Step 1: As in the question it is given that the particle starts moving from point A where track AB is frictionless and then from point B to C where track BC is frictional track with coefficient of friction\[\mu \].
Let us consider that the initial velocity of the particle (say mass of the particle is \[m\]) is \[\mathop v\nolimits_0 \]and initial height from which the particle starts moving along the given track, is \[h\].
                                   

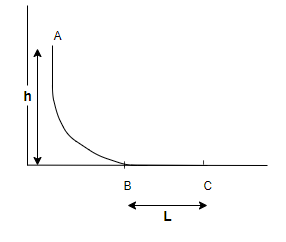
Step 2: From the above figure we can see that –
Total energy of the ball at point A will be equal to the sum of kinetic energy at that point and potential energy at that point. So, total energy can be written as –
Total energy at A = kinetic energy + potential energy
\[\mathop {\left( {\mathop E\nolimits_t } \right)}\nolimits_A = \dfrac{1}{2}m\mathop v\nolimits_0^2 + mgh\] …………………………..(1)
We know that energy is conserved in any closed system so the total energy at point B will be –
\[\mathop {\left( {\mathop E\nolimits_t } \right)}\nolimits_B = \dfrac{1}{2}m\mathop v\nolimits_0^2 + mgh\] …………………………..(2)
Step 3: Now, we know that friction opposes the relative motion of the ball so the energy that is at point B will be used against the work done by the frictional force while the particle is moving from point B to C.
But we know that frictional force is equal to the frictional coefficient \[\mu \] times the normal force on the body (i.e., R).
So, \[F = \mu R\]; where \[R = mg\], and \[m = \] mass of the body, and \[g = \]acceleration due to gravity
\[F = \mu mg\].........................................(3)
So, from the definition of work done against the frictional force –
\[W = F \times S\]; where \[S = L = \]distance covered by body from point B to C
Substituting the value from equation (3), we will get –
\[W = \mu mgL\] …………………………...(4)
Now, from the energy conservation law –
\[\mathop {\left( {\mathop E\nolimits_t } \right)}\nolimits_A \] or \[\mathop {\left( {\mathop E\nolimits_t } \right)}\nolimits_B = \] \[W\]
So, from equation (2) and (4), we will get –
\[\dfrac{1}{2}m\mathop v\nolimits_0^2 + mgh = \mu mgL\], on rearranging this equation
\[L = \dfrac{h}{\mu } + \dfrac{{\mathop v\nolimits_0^2 }}{{2\mu g}}\]

So, the correct option is (B).

Note:
-While solving these types of problems one should always remember that friction is a non-conservative force, i.e. work done against friction is path dependent.
-In the presence of friction, some energy is always lost in the form of heat etc. Because of the reason we can say mechanical energy is not conserved.