Question

A small ball is suspended from point O by a thread of length $l$. A nail is driven into the wall at a distance of $\dfrac{l}{2}$ below O, at A. The ball is drawn aside so that the thread takes up a horizontal position at the level of point O and then released. Find
(a) At what point of the ball’s trajectory, will the tension in the thread disappear?
(b) What will be the highest point to which it will rise?

Answer 1

Hint: Use conservation of energy formula to find the height of point P of the ball’s trajectory where the tension in the tread disappears. Find the velocity at point P and using this find the height from P. Add this height to the height of point P to find the highest point to which it will rise.

Complete step by step answer:

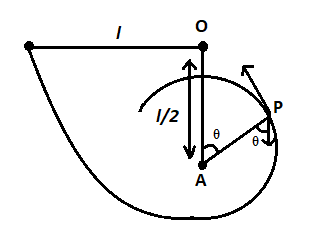
We are given that A small ball is suspended from point O by a thread of length $l$. A nail is driven into the wall at a distance of $\dfrac{l}{2}$ below O, at A and the ball is drawn aside so that the thread takes up a horizontal position at the level of point O and then released.
A) At what point of the ball’s trajectory, will the tension in the thread disappear?
At point P, the tension will be zero.
Then $mg\cos \theta = \dfrac{{mv_p^2}}{r}$
Using conservation of energy, $v_p^2 = gl\left( {1 - \cos \theta } \right)$
$
  v_p^2 = gl\left( {1 - \cos \theta } \right) \\
  \Rightarrow mg\cos \theta = \dfrac{{mv_p^2}}{r} \\
  \Rightarrow mg\cos \theta = \dfrac{{mgl}}{r}\left( {1 - \cos \theta } \right) \\
  r = \dfrac{l}{2} \\
  \Rightarrow mg\cos \theta = \dfrac{{mgl}}{{\dfrac{l}{2}}}\left( {1 - \cos \theta } \right) \\
  \Rightarrow mg\cos \theta = 2mg\left( {1 - \cos \theta } \right) \\
  \Rightarrow \cos \theta = 2 - 2\cos \theta \\
  \Rightarrow 2 = 3\cos \theta \\
  \Rightarrow \cos \theta = \dfrac{2}{3} \\
 $
Height of the point P is $\dfrac{l}{2} + \dfrac{l}{2}\cos \theta $
$
  \dfrac{l}{2} + \dfrac{l}{2}\cos \theta \\
  \cos \theta = \dfrac{2}{3} \\
  \Rightarrow height = \dfrac{l}{2} + \dfrac{l}{2} \times \dfrac{2}{3} \\
  \Rightarrow height = \dfrac{{5l}}{6} \\
 $
At $\dfrac{{5l}}{6}$ point of the ball’s trajectory, the tension in the thread will disappear.
B) What will be the highest point to which it will rise?
$
  v_p^2 = gl\left( {1 - \cos \theta } \right) \\
  \cos \theta = \dfrac{2}{3} \\
  \Rightarrow v_p^2 = gl\left( {1 - \dfrac{2}{3}} \right) \\
  \Rightarrow v_p^2 = gl\left( {\dfrac{1}{3}} \right) \\
  \Rightarrow v_p^2 = \dfrac{{gl}}{3} \\
  \Rightarrow {v_p} = \sqrt {\dfrac{{gl}}{3}} \\
 $
Now the particle describes the parabolic path. The height attained by the particle, from point P is
$
  h = \dfrac{{{{\left( {{v_p}\sin \theta } \right)}^2}}}{{2g}} \\
  \cos \theta = \dfrac{2}{3} \\
  \sin \theta = \sqrt {1 - {{\cos }^2}\theta } = \sqrt {1 - \dfrac{4}{9}} = \dfrac{{\sqrt 5 }}{3} \\
  \Rightarrow h = \dfrac{{\dfrac{{gl}}{3} \times \dfrac{5}{9}}}{{2g}} \\
  \Rightarrow h = \dfrac{{5gl}}{{54g}} = \dfrac{{5l}}{{54}} \\
 $
Add this to the height to the height of point P.

The height of highest point will be $\dfrac{{5l}}{6} + \dfrac{{5l}}{{54}} = \dfrac{{45l + 5l}}{{54}} = \dfrac{{50l}}{{54}}$
The height of the highest point to which it will rise is $\dfrac{{50l}}{{54}}$

Note:Tension is a force pulling something apart, such as a force pulling apart on the ends of a rope. You often calculate tension in pulley problems. A force is a more general term applying to pushing or pulling on something. So do not confuse tension with force.