Question

A slightly conical wire of length $L$ and end radii ${r_1}$ and ${r_2}$ is stretched by a force $F$ and $F$ applied parallel to the length in opposite directions and normal to the end faces. If $Y$ denotes young’s modulus, then the extension produced is:
A. $\dfrac{{FL}}{{\pi {r_1}{r_2}Y}}$
B. $\dfrac{{FLY}}{{\pi {r_1}{r_2}}}$
C. $\dfrac{{FL}}{{\pi {r_1}Y}}$
D. $\dfrac{{FL}}{{\pi r_1^2Y}}$

Answer 1

Hint: here, we will consider a conical wire of length $L$ . Both the ends of the wire are of different radius which are ${r_1}$ and ${r_2}$. Now, for calculating the extension produced in the wire we will consider a small element $dx$ . The extension produced by the whole can be calculated by integrating the extension produced in the small element.

Complete step by step answer:
Consider a slightly conical wire having length $L$. Let the radii of this conical wire are ${r_1}$ and ${r_2}$. Let this wire be stretched by a force $F$ which is applied parallel to the length of the wire in the opposite direction.

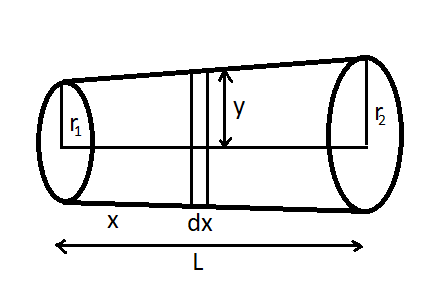
Now, let $R$ be the rate of change of the radius of the wire per length and is given by
$R = \dfrac{{{r_2} - {r_1}}}{L}$
Now consider a small element $dx$ that is at a distance of $x$ from the narrow part of the wire. Therefore, the radius of this element is given by
$y = {r_1} + Rx$
Now, the extension in the small element $dx$ is given by
$dI = \dfrac{{F\,dx}}{{\left( {\pi {y^2}} \right)Y}}$
$ \Rightarrow \,dI = \dfrac{{Fdx}}{{\pi Y{{\left( {{r_1} + Rx} \right)}^2}}}$
Thus, extension in the whole of the wire can be calculated by integrating the above equation between the limits $0$ to $L$ as shown below
$I = \dfrac{F}{{\pi Y}}\int\limits_0^L {\dfrac{{dx}}{{{{\left( {{r_1} + Rx} \right)}^2}}}} $
Now, put ${r_1} + Rx = p$
$ \Rightarrow \,Rdx = dp$
Also, the length of the whole conical wire is given by
$L = {r_1} + RL$
Now, putting both the values in $I$ , we get
$I = \dfrac{F}{{\pi Y}}\int\limits_{{r_1}}^{{r_1} + RL} {\dfrac{{\dfrac{{dp}}{R}}}{{{p^2}}}} $
$ \Rightarrow \,I = \dfrac{F}{{\pi Y}}\int\limits_{{r_1}}^{{r_1} + RL} {\dfrac{{dp}}{{R{p^2}}}} $
$ \Rightarrow \,I = \dfrac{F}{{\pi YR}}\int\limits_{{r_1}}^{{r_1} + RL} {\dfrac{{dp}}{{{p^2}}}} $
$ \Rightarrow \,I = \dfrac{F}{{\pi YR}}\left[ {\dfrac{1}{p}} \right]_{{r_1}}^{{r_1} + RL}$
Now, putting the limits we get
$I = \dfrac{F}{{\pi YR}}\left[ {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_1} + RL}}} \right]$
$ \Rightarrow \,I = \dfrac{F}{{\pi YR}}\left[ {\dfrac{{{r_1} + RL - {r_1}}}{{{r_1}\left( {{r_1} + RL} \right)}}} \right]$
$ \Rightarrow \,I = \dfrac{F}{{\pi YR}}\left[ {\dfrac{{RL}}{{{r_1}\left( {{r_1} + RL} \right)}}} \right]$
Now, putting the value of $R$ or $RL$ , we get
$ \Rightarrow \,I = \dfrac{{FL}}{{\pi Y\left( {{r_2} - {r_1}} \right)}}\left[ {\dfrac{{{r_2} - {r_1}}}{{{r_1}({r_1} + {r_2} - {r_1})}}} \right]$
$ \Rightarrow \,I = \dfrac{{FL}}{{\pi Y\left( {{r_2} - {r_1}} \right)}}\left[ {\dfrac{{{r_2} - {r_1}}}{{{r_1}({r_1} + {r_2} - {r_1})}}} \right]$
$ \Rightarrow \,I = \dfrac{{FL}}{{\pi Y}}\left[ {\dfrac{1}{{{r_1}{r_2}}}} \right]$
$ \Rightarrow \,I = \dfrac{{FL}}{{\pi Y{r_1}{r_2}}}$
Therefore, the extension produced in the wire is $\dfrac{{FL}}{{\pi Y{r_1}{r_2}}}$ .

So, the correct answer is “Option A”.

Note:
Here, we have changed the limit $0$ in the equation to ${r_1}$. This is because we have changed the function of integration from $y$ to $p$ . this can be done as shown below
Putting $x = 0$ , because the lower limit is zero, in the equation of $y$
$y = {r_1} + R \times 0$
$ \Rightarrow \,y = {r_1}$
In this way, the lower limit of integration becomes ${r_1}$ .