Question

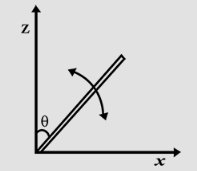
A slender uniform rod of mass $M$ and length $l$ is pivoted at one end so that it can rotate in a vertical plane. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle $\theta $ with the vertical is

A. $\dfrac{{2g}}{{3l}}\cos \theta $
B. $\dfrac{{3g}}{{2l}}\sin \theta $
C. $\dfrac{{2g}}{{3l}}\sin \theta $
D. $\dfrac{{3g}}{{2l}}\cos \theta $

Answer 1

Hint: At initial the rod is placed vertically and after some time it tends to rotate with axis as origin. Then the torque on the rod is defined by the product of force on the rod which tends to move it and the perpendicular distance between the line of action of force to the axis of rotation. The torque is also defined as the product of moment of inertia and the angular acceleration of the rod. By equating the toque, the angular acceleration of the rod is derived.

Useful formula:
The torque on the rod with respect to force is given by,
$\tau = F \times d$
Where, $\tau $ is the torque on the rod, $F$ is the force on the rod which tends to rotate and $d$ is the perpendicular distance between the line of action of force to the axis of rotation.

The torque on the rod with respect to acceleration is given by,
$\tau = I \times \alpha $
Where, $\tau $ is the torque on the rod, $I$ is the moment of inertia on the rod and $\alpha $ is the angular acceleration of the rod.

Given data:
The mass of the rod is $M$
The length of the rod is $l$
The angle between the rod and the vertical axis is $\theta $

Complete step by step solution:

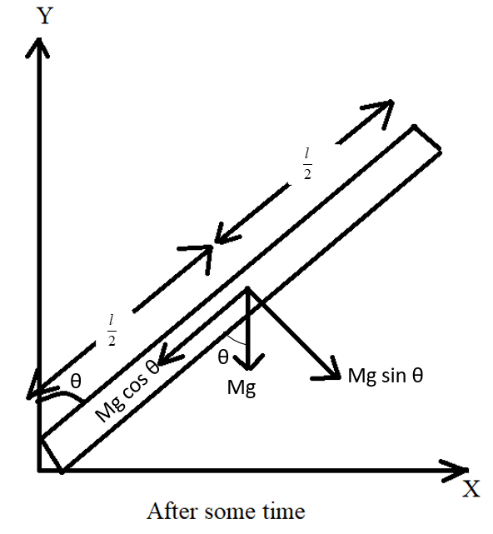
The force acting downward due to the weight of the body is given by,
$F = mg$
Where, $m$ is the mass of the rod and $g$ is the acceleration due to gravity.
By resolving the force with respect to the given angle $\theta $, we get
${F_1} = mg\cos \theta $ which is along the length of the rod and ${F_2} = mg\sin \theta $ which is perpendicular to the rod.

Since, the force ${F_2}$ drives the rod to rotate.
Thus, the torque on the rod with respect to the force ${F_2}$ is given by,
$\tau = {F_2} \times d$
Substitute the values of ${F_2}$ and $d = \dfrac{l}{2}$ in above equation, we get
$\tau = mg\sin \theta \times \dfrac{l}{2}\;............................................\left( 1 \right)$

The moment of inertia of the rectangular rod is given by,
$I = \dfrac{{m{l^2}}}{3}$
And the angular acceleration of the rod is $\alpha $
The torque of rod with respect to angular acceleration of the rod is given by,
$\tau = I \times \alpha $
Substitute the values of $I$ and $\alpha $ in above equation, we get
$\tau = \dfrac{{m{l^2}}}{3} \times \alpha \;...............................................\left( 2 \right)$

By equation (1) and (2), we get
$
  mg\sin \theta \times \dfrac{l}{2} = \dfrac{{m{l^2}}}{3} \times \alpha \\
  \alpha = mg\sin \theta \times \dfrac{l}{2} \times \dfrac{3}{{m{l^2}}} \\
 $
BY cancelling the common terms in RHS,
$
  \alpha = g\sin \theta \times \dfrac{3}{{2l}} \\
  \alpha = \dfrac{{3g\sin \theta }}{{2l}} \\
 $

Hence, the option (B) is correct.

Note: The torque on the rod of the two conditions, one is respect to force and another one is respect to the angular acceleration are same. The resolved force along the length of the rod will not produce any torque on the rod because the line of action of that force is on the origin point.