Question

A sledge car of mass $m$ fitted with a rocket booster is moving on a frictionless horizontal ice surface with initial velocity $\overrightarrow{u}$ parallel to the $\text{x-axis}$ at a distance $d$. Rocket boosters are fired for $1\text{ sec}$ producing a velocity $\overrightarrow{v}$ in the sledge car parallel to the $\text{x-axis}$. The magnitude of the torque which acted about the origin of coordinates is
A.) Zero
B.) $m\left( v-u \right)d$
C.) $mud$
D.) $mvd$

Answer 1

Hint: This problem can be solved by finding out the change in the angular momentum of the body about the origin. Since the torque acting on a body is nothing but the rate of change of angular momentum, we will get the torque on the body about the origin.
 Formula used:

Average torque $\overrightarrow{\tau }$ acting on a body is equal to the rate of change of angular momentum $\overrightarrow{L}$ of the body.
$\overrightarrow{\tau }=\dfrac{\Delta \overrightarrow{L}}{\Delta t}$
where $\Delta t$ is the time period for which the torque acts.
The angular momentum $\overrightarrow{L}$ of a body of mass $m$ about a point is given by
$\overrightarrow{r}\times m\overrightarrow{v}$
where $\overrightarrow{r}$ is the vector joining the point to the body and $\overrightarrow{v}$ is the velocity of the body.

Complete step by step answer:
As explained in the hint, we will find the change in the angular momentum of the body about the origin in the given time and use the ratio to get the average torque action upon the body about the origin in that time period.
Let us draw a diagram to analyze the question better.

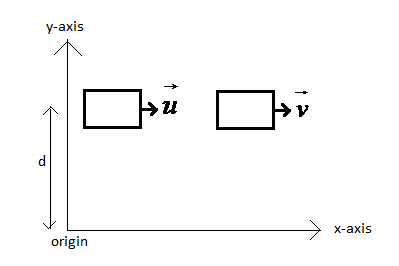
Let unit vectors along the x and y axes be $\widehat{i}$ and $\widehat{j}$ respectively.
Let the magnitudes of the initial and final angular momenta be ${{L}_{i}}$ and ${{L}_{f}}$ respectively.
Let the magnitude of torque on the body about the origin be $\tau $ and the time period is $t=1s$.

The angular momentum $\overrightarrow{L}$ of a body of mass $m$ about a point is given by
$\overrightarrow{L}=\overrightarrow{r}\times m\overrightarrow{v}$ --(1)
where $\overrightarrow{r}$ is the vector joining the point to the body and $\overrightarrow{v}$ is the velocity of the body.
Now, since (1) is a cross product, the magnitude of the resultant will be due the product of the velocity and the component of the radial distance to the vector that is perpendicular to the velocity. Hence, it will manifest itself in the distance of the body from the origin along the y-axis (velocity is along the x-axis). This required distance is given to be $d$ as shown in the figure.
$\therefore \left| \overrightarrow{L} \right|=mv{{r}_{\bot }}$ --(2)
where ${{r}_{\bot }}$ denotes the distance of the body from the origin perpendicular to the velocity, that is along the y-axis.

Let the magnitudes of the initial and final velocity be $u$ and $v$ respectively.
Therefore, using (2), we get,
${{L}_{i}}=mud$
${{L}_{f}}=mvd$
The change $\Delta L$ in the angular momentum will be
$\Delta L={{L}_{f}}-{{L}_{i}}$
$\therefore \Delta L=mvd-mud=m\left( v-u \right)d$ --(3)
Now, the required time period is $\Delta t=1s$.
Average torque $\overrightarrow{\tau }$ acting on a body is equal to the rate of change of angular momentum $\overrightarrow{L}$ of the body.
$\overrightarrow{\tau }=\dfrac{\Delta \overrightarrow{L}}{\Delta t}$ --(4)
where $\Delta t$ is the time period for which the torque acts.
Using (4), we get,
$\overrightarrow{\left| \tau \right|}=\dfrac{\left| \Delta \overrightarrow{L} \right|}{\Delta t}$
Hence, using (3), we get,
$\tau =\dfrac{m\left( v-u \right)d}{1}=m\left( v-u \right)d$
Hence, the torque about the origin on the body is $m\left( v-u \right)d$.

Hence, the correct option is B) $m\left( v-u \right)d$.

Note: Students might think that the radial distance of the body is changing due to the change in velocity of the body (implying acceleration). However, even though this is true, they must realize that the perpendicular distance remains the same since the body moves parallel to the x-axis and hence the component of the radial distance perpendicular to the initial and final velocity remains constant throughout. This makes the problem much simpler and students must quickly notice this to solve the problem faster. However, this is only applicable in this problem, since the initial and final velocities were in the same parallel direction. If the direction between the initial and final velocities were to change the problem would become a bit harder as the perpendicular component of the radial distance would also change.