Question

A Single wire \[ABC\] passes through a ring $C$ which revolves a constant speed in the horizontal circle of radius $r$ as shown in the figure. The speed of revolution is.

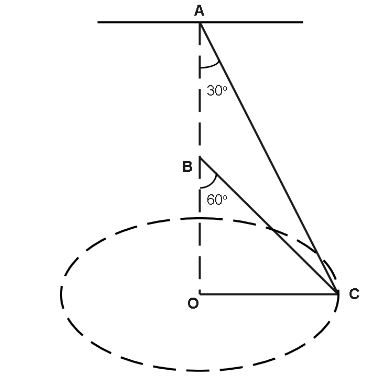
Answer 1

Hint: To solve this question first one must have a concept of Newton’s law of motion. Here we first draw the diagram where we have resolved all the forces and the solved to obtain the equation and the solved for centripetal force and the equated both the equation to get our required solution.

Formula used:
${F_c} = \dfrac{{m{v^2}}}{r}$
Where, ${F_c}$ is the centripetal force, $m$ is the mass, $r$ is the radius and $v$ is the velocity.

Complete step by step answer:
Let us draw the all the forces of acting on the diagram of the given figure,

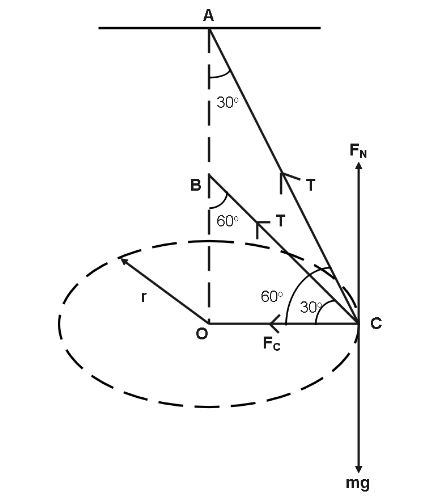
From the figure we can say that,
\[{F_N} = Mg\]
And we can write the above equation as,
$T\sin {30^ \circ } + T\sin {60^ \circ } = mg \\
\Rightarrow \dfrac{T}{2} + \dfrac{{\sqrt 3 }}{2}T = mg $
And on further simplifying we can write,
$ \Rightarrow \dfrac{T}{2} + \dfrac{{\sqrt 3 }}{2}T = mg$
$ \Rightarrow \left( {\sqrt 3 + 1} \right)\dfrac{T}{2} = mg$ -----(1)

And we know that centripetal force is given by,
${F_c} = \dfrac{{m{v^2}}}{r}$
So, we can write as,
\[T\sin {30^ \circ } + T\sin {60^ \circ } = \dfrac{{m{v^2}}}{r} \\
\Rightarrow \dfrac{{\sqrt 3 T}}{2} + \dfrac{T}{2} = \dfrac{{m{v^2}}}{r} \\ \]
On further solving,
\[\Rightarrow \dfrac{{\sqrt 3 T}}{2} + \dfrac{T}{2} = \dfrac{{m{v^2}}}{r} \\
\Rightarrow \left( {\sqrt 3 + 1} \right)\dfrac{T}{2} = \dfrac{{m{v^2}}}{r} \\ \]
And now the final step substituting the value of \[\left( {\sqrt 3 + 1} \right)\dfrac{T}{2}\] from equation 1 in the above obtained equation,
\[\left( {\sqrt 3 + 1} \right)\dfrac{T}{2} = \dfrac{{m{v^2}}}{r} \\
\Rightarrow mg = \dfrac{{m{v^2}}}{r} \\
\Rightarrow {v^2} = rg \\
\therefore v = \sqrt {rg} \\ \]
Hence, the speed of revolution is \[\sqrt {rg} \].

Note: The centripetal force acting on the body should not be confused with the centrifugal force acting on the body. Although both forces are nearly identical, the key distinction is that the centripetal force acts in the direction of the circular path's centre of curvature, whereas the centrifugal force acts in the opposite direction. As a result, students should be aware of the distinction before attempting to solve the problem.