Question

A simple pendulum with length L and mass of the bob is vibrating with an amplitude a. Then the maximum tension in the string is:
$
  {\text{A}}{\text{. }}mg \\
  {\text{B}}{\text{. }}mg\left[ {1 + {{\left( {\dfrac{a}{L}} \right)}^2}} \right] \\
  {\text{C}}{\text{. }}mg{\left[ {1 + \dfrac{a}{{2L}}} \right]^2} \\
  {\text{D}}{\text{. }}mg{\left[ {1 + \left( {\dfrac{a}{L}} \right)} \right]^2} \\
$

Answer 1

Hint: The tension in the string of the pendulum has maximum value at the mean position of the pendulum and is equal to the sum of the weight of the pendulum and centripetal force acting on the pendulum.

Formula used:
Gravitational force on an object of mass m is given as:
$F = mg$

The centripetal force for an object of mass m moving in a circular orbit of radius r with velocity v has the following formula:

$F = \dfrac{{m{v^2}}}{r}$

The frequency of a pendulum or angular velocity is given as

$\omega = \sqrt {\dfrac{g}{L}} {\text{ }}...{\text{(i)}}$

Angular velocity is related to linear velocity as

${\text{v}} = r\omega {\text{ }}...{\text{(ii)}}$

Complete step-by-step answer:
A simple pendulum consists of a bob oscillating to and fro its mean position. The following diagram shows a pendulum’s mean and extreme position with the various forces acting on the pendulum in the two positions. The length of the pendulum is L and T is the tension in the string due to the weight of the bob.

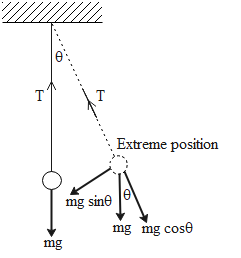
The tension in the string of the pendulum is equal to the weight of the bob. When the bob is at its mean position, its weight mg creates tension in the bob whereas when it is at its extreme position, only a component or a part of weight of the bob (mg cos$\theta $) acts on the string. Due to this reason, the tension in the pendulum is maximum at the mean position.

The pendulum moves in a semicircle. The necessary centripetal force is provided by the tension T. The radius of this semi-circle is equal to the length of the pendulum.

Using the above information, we can write the expression for maximum tension in the string as

${T_{\max }} = mg + \dfrac{{m{v^2}}}{L}{\text{ }}...{\text{(iii)}}$
Now, using equation (ii) in (i), we get

${\text{v}} = a\omega $

where a is the amplitude of vibration
${\text{v}} = a\sqrt {\dfrac{g}{l}} $

Using this expression in equation (iii), we get

$
  {T_{\max }} = mg + \dfrac{m}{L}\left( {\dfrac{{{a^2}g}}{L}} \right) \\
   = mg + \dfrac{{m{a^2}g}}{{{L^2}}} \\
   = mg\left( {1 + \dfrac{{{a^2}}}{{{L^2}}}} \right) \\
$

Hence the correct answer is option B.

Note:
1. A component of a vector always has a smaller magnitude than the vector itself.
2. A body requires centripetal force to move in a circular orbit. Here the tension provides this centripetal force to the pendulum.