Question

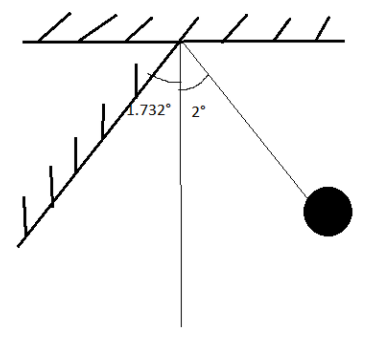
A simple pendulum of length $1m$ is allowed to oscillate with amplitude \[2^\circ \]. It collides elastically with a wall inclined at \[1.732^\circ \] to the vertical. Its time period will be : (use \[g{\text{ }} = {\text{ }}{\pi ^2}\]).

A.\[\dfrac{2}{3}sec\]
B.\[\dfrac{4}{3}sec\]
C.3 sec
D.\[\dfrac{5}{3}sec\]

Answer 1

Hint: Simple harmonic motion: A motion is said to be simple harmonic if restoring force or acceleration is directly proportional to the displacement or amplitude from its mean position.
i.eRestoring force is directly proportional to displacement for oscillating spring and restoring force is directly proportional to angular displacement or amplitude for oscillating pendulum as shown below.

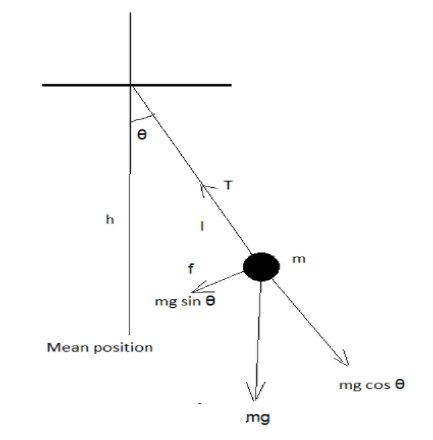
The time period of the simple pendulum is defined as the time needed to complete one oscillation for a pendulum.
For a simple pendulum, the time period will only depend on its length and acceleration due to gravity for some small angular amplitude or angular displacement \[\theta \].
Formula Used:
$T = 2\pi \sqrt {\dfrac{l}{g}} $
\[x{\text{ }} = {\text{ }}{x_0}sin{\text{ }}\left( {\omega t} \right)\]

Complete answer:
Given that,
Length of a simple pendulum, \[l = 1m\]
Acceleration due to gravity, \[g = {\pi ^2}\]
Maximum amplitude, \[{x_0} = 2^\circ \]
The angle of inclination of a wall or final amplitude when a ball hit the wall at a time “$t$ ”, x = \[x = 1.732^\circ \]
From the above explanation, we know that time needed to complete one oscillation for a pendulum is given as
$T = 2\pi \sqrt {\dfrac{l}{g}} $
By substituting the given value of g and l we get
$T = 2\pi \sqrt {\dfrac{1}{{{{{\pi }}^2}}}} = \dfrac{{2\pi }}{\pi } = 2sec$
Therefore time needed to reach the mean position will be half of the total time period
i.e., \[{t_1} = 1sec\]
Now time needed to cover \[1.732^\circ \] can be predicted using the equation of simple harmonic motion
i.e., \[x{\text{ }} = {\text{ }}{x_0}sin{\text{ }}\left( {\omega t} \right)\]
By substituting the given values we get
$ \Rightarrow 1.72 = 2 \times \sin \left( {\dfrac{{2\pi }}{T} \times t} \right)$ ….. ( angular frequency, \[\omega = \dfrac{{2\pi }}{T}\])
$ \Rightarrow \dfrac{{2\pi }}{2} \times t = {\sin ^{ - 1}}\left( {\dfrac{{1.72}}{2}} \right)$
Hence the total time in which the pendulum get back to its mean position is given as
${T_{total}} = {t_1} + 2{t_2} = 1 + \dfrac{2}{3} = \dfrac{5}{3}sec$

Note:
For simple harmonic motion, restoring force always brings back pendulum to its mean position hence in the final equation we have considered that the total time period of oscillation will be the sum of time needed during the first half “\[{t_1}\] ” and after bouncing back the pendulum will complete one oscillation hence twice of the second half.
Also, we must note that if there is no external force acting on a pendulum the time period will only depend on length, if we consider g and constant, irrespective of its mass, shape, size, and initial velocity.