Question

A simple pendulum is set up in a trolley which moves to the right with an acceleration on a horizontal plane. Then the thread of the pendulum in the mean position makes an angle $\theta$ with the vertical.

Answer 1

Hint: In this question we will use the relation between the force acting on the pendulum and the angle made by the pendulum, further, by solving this we will get the required result. Also, we will learn the basics of a simple pendulum for our better understanding.
Formula used:
 $\tan \theta = \left( {\dfrac{{ma}}{{mg}}} \right)$

Complete answer:
Due to horizontal acceleration, a pseudo force acts on the bob of the pendulum in horizontal direction, backwards. Below is the diagram of a simple pendulum, having mass of bob m, length of string L and oscillation angle $\theta$ :

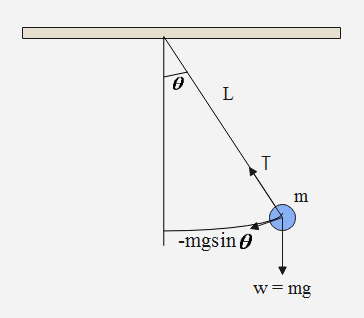
Also, here the gravitational force mg acts on it vertically downwards. So, the angle that the thread makes with vertical is given by:
$\tan \theta = \left( {\dfrac{{ma}}{{mg}}} \right)$
$ \Rightarrow \theta = {\tan ^{ - 1}}\left( {\dfrac{{ma}}{{mg}}} \right)$
Further, by solving this, we get:
$\therefore \theta = {\tan ^{ - 1}}\left( {\dfrac{a}{g}} \right)$
Therefore, we get the required result of the angle that the thread makes with vertical.

Additional information:
We will now discuss the basic definition of a simple pendulum and a compound pendulum.
A simple pendulum is represented by a mass of no size attached to a string of with no mass. A compound pendulum represents a real object that is swinging about a point other than its center of gravity.
Since we know that the two pendulums differ from each other, one difference between them is that the simple pendulum is the only physical property that affects its period is its length. The mass of the object does not affect the period whereas, in compound pendulum the object’s mass and how that mass is distributed both of them are important in determining the period.

Note:
We should remember that a simple pendulum is different from compound pendulum. The time period and other factors like its length affect the simple pendulum. We should remember how these physical quantities varies in simple pendulum