Question

A simple pendulum is released from horizontal position as shown in figure. For what value of $\alpha $ (angle between string and vertical) during its motion, the total acceleration is directed horizontally?

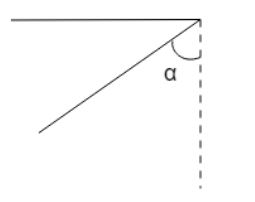
A. ${0^ \circ }$
B. ${90^ \circ }$
C. ${\cos ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right)$
D. ${\cos ^{ - 1}}\left( {\dfrac{1}{2}} \right)$

Answer 1

Hint: Firstly we are going to make a free body diagram of the given simple pendulum. Now, we are going to find the normal and the tangential acceleration by resolving the acceleration acting on the pendulum. At last, we are going to find the value of $\alpha $ (angle between string and vertical) by using trigonometric functions.

Complete step by step answer:
The free body diagram of the given question is,

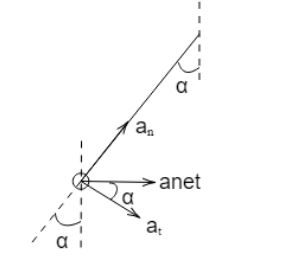
In the above figure, ${a_n}$ is the normal component of acceleration, ${a_t}$ is the tangential component of acceleration, ${a_{net}}$ is the net acceleration which is acting and $\alpha $ is the angle between string and vertical. From the figure, we can clearly see that,
$\tan \alpha = \dfrac{{{a_n}}}{{{a_t}}}.....(1)$
Now, we need to find out the value of ${a_n}$ and ${a_t}$, in order to get the value of the above expression.From the figure we can clearly see that the tangential acceleration ${a_t}$ is equal to the $g\sin \alpha $. So, ${a_t} = g\sin \alpha .....(2)$
We can clearly see that ${a_n}$ is centripetal acceleration. So,
${a_n} = \dfrac{{{v^2}}}{R}......(3)$

On applying the law of conservation of energy, we can say that,
$\dfrac{1}{2}m{v^2} = mgR\cos \alpha $
When we cancel the common terms on both the sides, we get,
$\dfrac{{{v^2}}}{R} = 2g\cos \alpha $
On putting the above value in equation (3), we get,
${a_n} = 2g\cos \alpha ......(4)$
On putting the value of ${a_n}$ and ${a_t}$ from equation (4) and equation (2), in equation (1), we get,
$\tan \alpha = \dfrac{{2g\cos \alpha }}{{g\sin \alpha }}$

On cancelling the common terms in the denominator, we get,
$\tan \alpha = \dfrac{{2\cos \alpha }}{{\sin \alpha }}$
On further solving we get,
${\tan ^2}\alpha = 2$
When we take square root on both the sides, we get,
$\tan \alpha = \sqrt 2 $
Now, on calculating the value of $\cos \alpha $ from $\tan \alpha $, we get,
$\cos \alpha = \dfrac{1}{{\sqrt 3 }}$
Now on taking the inverse of this trigonometric function, we get,
$\therefore \alpha = {\cos ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right)$

So, the correct answer is C.

Note: To solve such questions, we need to understand the concept of normal and tangential acceleration. Tangential acceleration is defined as the measure of the time rate of change in the magnitude of the velocity vector whereas normal acceleration is defined as a measure of the time rate of change of the direction of the given velocity vector.