Question

A simple pendulum having a bob of mass m undergoes small oscillations with amplitude ${\theta _o}$. Find the tension in the string as a function of the angle made by the string with the vertical?

Answer 1

Hint: In order to solve this question, we need to get two equations of forces which are acting on this system. The equation comes from the law of conservation of energy and the second equation comes from the centripetal force acting on the bob. On solving these two equations, we will get the required answer.

Complete step by step answer:
The diagram required to understand question is:

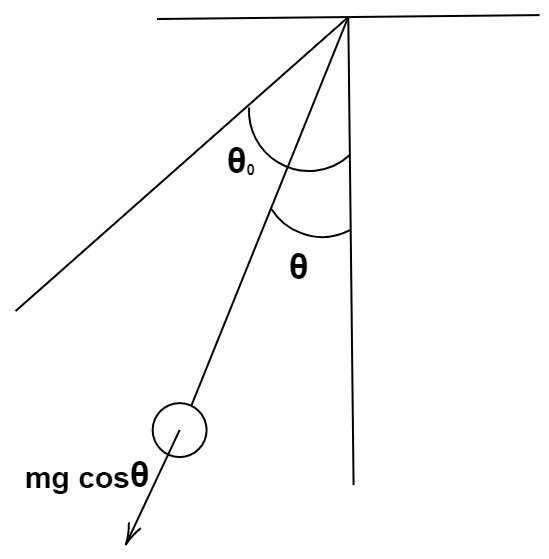
In this question, the forces which are acting on the bob are weight and the tension due to the string. Now, this bob moves in a circular path and its acceleration has both tangential and radial component.
Let us consider that the speed of the bob at an angle $\theta $ is $v$. Now, we will use the law of conservation of energy on two points. These two points are the extreme point and the point that makes an angle $\theta $.
$\dfrac{1}{2}m{v^2} = mgl(\cos \theta - \cos {\theta _o})$
On rearranging the above equation, we get,
$\dfrac{{m{v^2}}}{l} = 2mg(\cos \theta - \cos {\theta _o}).......(1)$
Also, as the bob moves in a circular direction, so a centripetal force acts on it which acts towards the centre. The value of this centripetal force is $\dfrac{{m{v^2}}}{l}$. Thus,
\[T - mg\cos \theta = \dfrac{{m{v^2}}}{l}\]
By replacing the value of $\dfrac{{m{v^2}}}{l}$ from equation (1), we get,
$T - mg\cos \theta = 2mg(\cos \theta - \cos {\theta _o})$
$T - mg\cos \theta = 2mg\cos \theta - 2mg\cos {\theta _o}$
On keeping $T$ on one side and taking all the other terms on other side, we get,
$T = 2mg\cos \theta + mg\cos \theta - 2mg\cos {\theta _o}$
$T = 3mg\cos \theta - 2mg\cos {\theta _o}$
So, the tension in the string as a function of the angle made by the string with the vertical is $T = 3mg\cos \theta - 2mg\cos {\theta _o}$.

Note:
It is important to note that for a body to move in a circular direction, the action of the centripetal force is required. In case of a pendulum, this centripetal force is provided by the tension which is present in the string. As the centripetal force stops acting on a body, the circular motion of the body also comes to a stop.