Question

A sign board in the shape of a triangle has length of $ 10\;cm $ , $ 16\;cm $ and $ 20\;cm $ . A poster is to be made to cover the sign board. Find the area of the poster.

Answer 1

Hint: Firstly find the area of the triangle with the given side lengths of the triangle and the poster is to be made of the same area as that of triangle. In that way we will get the area of the poster.

Complete step-by-step answer:
A sign board in the shape of a triangle has length of $ 10\;cm $ , $ 16\;cm $ and $ 20\;cm $ . A poster is to be made to cover the sign board.

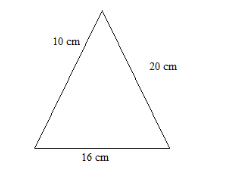
The Heron’s formula for the area of the triangle with given side lengths of the triangle as $ a $ , $ b $ and $ c $ is equal to $ \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ , where $ s $ is the semi perimeter of the triangle and is equal to $ \dfrac{{a + b + c}}{2} $ .
Firstly find the semi perimeter of the triangle with the given side lengths:
 $
  s = \dfrac{{a + b + c}}{2} \\
   = \dfrac{{10 + 16 + 20}}{2} \\
   = \dfrac{{46}}{2} \\
   = 23\;cm \;
  $
Now substitute the values of $ s $ , $ a $ , $ b $ and $ c $ in the formula for the area of triangle.
 $
\Rightarrow A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} \\
   = \sqrt {23\left( {23 - 10} \right)\left( {23 - 16} \right)\left( {23 - 20} \right)} \\
   = \sqrt {23 \times 13 \times 7 \times 3} \\
   = \sqrt {6279} \\
   = 79.24\;c{m^2} \;
  $
The area of the given triangle is equal to $ 79.24\;c{m^2} $ . The area of the poster needed to cover will be equal to the area of the triangle.
So, the area of the poster is equal to $ 79.24\;c{m^2} $ .
So, the correct answer is “ $ 79.24\;c{m^2} $ ”.

Note: The Heron’s formula for the area of the triangle with given side lengths of the triangle as $ a $ , $ b $ and $ c $ is equal to $ \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ , where $ s $ is the semi perimeter of the triangle and is equal to $ \dfrac{{a + b + c}}{2} $ . Use the given side lengths of the triangle to find the area of the triangle.