Question

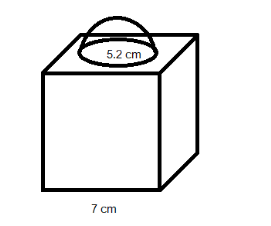
A show-piece shown in figure is made of two solids - a cube and a hemisphere. The base of the block is a cube with edge \[7\text{ }cm\] and the hemisphere fixed on the top has diameter \[5.2\text{ }cm\] . Find the total surface area of the piece.

Answer 1

Hint: To find the surface area of the entire figure, we need to first find the surface area of the cube and after that we will add the curved surface area of the half sphere or hemisphere and then subtract it by the area of the circle of the hemisphere to find the total surface area of the figure.
The surface area of a cube is: \[6{{a}^{2}}\]
The curved surface area of a hemisphere of half a sphere is: \[2\pi {{r}^{2}}\]
The total surface area of the figure is: \[6{{a}^{2}}+2\pi {{r}^{2}}\]
where \[a\] is the length of the edge of the cube and \[r\] is the radius of the hemisphere.

Complete step-by-step answer:
To find the total surface area of the figure let us find the surface area of the cube first with length of the edges as \[7\text{ }cm\] . We will use the formula of \6{{a}^{2}}\ and place the value of \[a\] as \[7\] , we get the value of the surface area of the cube as:
 \[\Rightarrow 6{{a}^{2}}\]
 \[\Rightarrow 6\times 7\times 7\]
 \[\Rightarrow 294\text{ }c{{m}^{2}}\]
Now with the surface area of the cube we move next to find the curved surface area of the hemisphere. Using the curved surface area of the hemisphere we find the surface area as:
The curved surface area of a hemisphere of half a sphere is: \[2\pi {{r}^{2}}\]
Placing the values in the above formula with \[\pi =3.14\] and radius \[r=\dfrac{5.2}{2}\] , we get the value as:
 \[\Rightarrow 2\pi {{r}^{2}}\]
 \[\Rightarrow 2\times 3.14\times {{\left( \dfrac{5.2}{2} \right)}^{2}}\]
 \[\Rightarrow 2\times 3.14\times {{\left( 2.6 \right)}^{2}}\]
 \[\Rightarrow 42.45\text{ }c{{m}^{2}}\]
After this we find the area of the circle on the top of the cube and subtract it from the sum of the surface area of the cube and hemisphere. Hence, the area of the circle is:
 \[\Rightarrow \pi {{r}^{2}}\]
 \[\Rightarrow 3.14\times {{\left( \dfrac{5.2}{2} \right)}^{2}}\]
 \[\Rightarrow 21.22\text{ }c{{m}^{2}}\]
Therefore, the total surface area of the figure is given;
Sum of the total surface area of the cube and curved surface of the hemisphere subtracted to area of the circle as:
 \[\Rightarrow 294\text{ }c{{m}^{2}}+42.45\text{ }c{{m}^{2}}-21.22\text{ }c{{m}^{2}}\]
 \[\Rightarrow 315.23\text{ }c{{m}^{2}}\]
So, the correct answer is “ \[ 315.23\text{ }c{{m}^{2}}\] ”.

Note: Students may go wrong if they add the surface area of the cube and hemisphere together as the area of the circle of the hemisphere is a part of the top surface of the cube and its area is already included in the area of the cube; hence, the total surface area of the figure is sum of the area of the two objects minus the common surface.