Question

a) Show, giving via suitable diagram, how unpolarized light can be polarized by reflection.
(b) Two polaroids \[{P_1}\] and \[{P_2}\] are placed with their pass axes perpendicular to each other. Unpolarised light of intensity I is incident on \[{P_1}\]. A third polaroid \[{P_3}\] is kept in between \[{P_1}\] and \[{P_2}\] such that its pass axis makes an angle of \[60^\circ \] with that of \[{P_1}\]. Determine the intensity of light transmitted through \[{P_1}\], \[{P_2}\] and \[{P_3}\]

Answer 1

Hint: The vertically vibrating of light is transmitted through a reflective surface, while the horizontal vibration is reflected. When an unpolarized light passes through the first polaroid, the intensity of the plane polarized light is half that of the incident unpolarised light.
Formula used: We will be using the following formula,
 \[I = \dfrac{{{I_0}}}{2}\] where \[I\] is the intensity of the polarized light transmitted through the first polaroid and \[{I_0}\] is the intensity of an unpolarized light. \[I = {I_0}{\cos ^2}\theta \] where \[I\] is the final intensity of the transmitted polarized light, \[{I_0}\] is the initial intensity a plane polarized light, and \[\theta \] is the angle the direction of polarization and the pass axis of the polaroid.

Complete Step-by-Step Solution:
a)

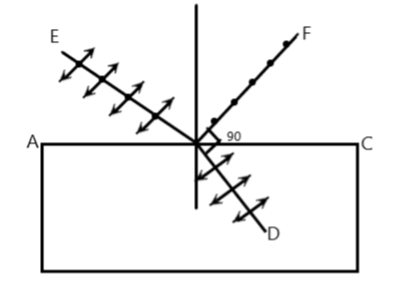
When unpolarized light E strikes a reflective surface AC, the vertically vibrating component of light becomes refracted into the block while the horizontal
(parallel to the surface) vibrating light F is reflected. When the angle of incidence is increased to an extent such that the angle between the reflected and the refracted ray is \[90^\circ \], a perfectly horizontally polarized light is reflected.
b) When the unpolarised light strikes the first polaroid, the resulting intensity becomes half that of the intensity of the unpolarized light. Therefore,
\[{I_1} = \dfrac{{{I_0}}}{2}\] where \[{I_1}\] is the intensity of the polarized light transmitted through \[{P_1}\].
The polarized light strikes a second polaroid \[{P_3}\] which is at angle \[60^\circ \] to \[{P_1}\]. Thus, intensity of the transmitted light is given by
\[{I_3} = {I_1}{\cos ^2}60\]
\[ \Rightarrow {I_3} = {I_1}{\left( {\dfrac{1}{2}} \right)^2} = \dfrac{{{I_1}}}{4}\]
where \[{I_3}\] is the intensity of the light transmitted through \[{P_3}\].
Since \[{I_1} = \dfrac{{{I_0}}}{2}\], then
\[{I_3} = \dfrac{{{I_0}}}{2} \times \dfrac{1}{4} = \dfrac{{{I_0}}}{8}\]
Finally, the intensity through \[{P_2}\] is given as
\[{I_2} = {I_3}{\cos ^2}30\] (angle of \[{P_3}\] with \[{P_2}\] will be \[90^\circ - 60^\circ \])
Hence,
\[{I_2} = \dfrac{{{I_0}}}{8}{\cos ^2}60 = \dfrac{{{I_0}}}{8}{\left( {\dfrac{{\sqrt 3 }}{2}} \right)^2} = \dfrac{{{I_0}}}{8} \times \dfrac{3}{4}\]
\[\therefore {I_2} = \dfrac{3}{{32}}{I_0}\]

Note: In application, the arrangement of polaroids as done in (b) is used when we need to rotate the direction of polarization by \[90^\circ \]like from vertical axis to horizontal axis. Without the polaroid \[{P_3}\] all light transmitted through \[{P_1}\] will be cut off by \[{P_2}\]since \[{I_2} = {I_0}{\cos ^2}90^\circ = 0\]. But when the polaroid \[{P_3}\]is placed, it allows some light to pass through \[{P_2}\] and with the direction rotated by \[90^\circ \].