Question

A ship is travelling due east at 10km/h. A ship heading 30$^\circ $ east of north is always due north from the first ship. The speed of the second ship in km/h is:
$
  {\text{A}}{\text{. }}20\sqrt 2 \\
  {\text{B}}{\text{. 20}}\sqrt {\dfrac{3}{2}} \\
  {\text{C}}{\text{. 20}} \\
  {\text{D}}{\text{. }}\dfrac{{20}}{{\sqrt 2 }} \\
$

Answer 1

Hint: A vector can be resolved into its components. This problem can be solved by resolving components of the velocities of the two ships. Equating components wherever possible may give us the required answer.

Step by step solution:

We have ship 1 travelling in the east direction with a speed of 10km/h.
${{\text{v}}_1} = 10km/h$

The ship 2 is travelling at an angle of 30$^\circ $ east of north direction with speed ${{\text{v}}_2}$. We need to find the velocity of the second ship with the available information. We can diagrammatically represent the situation as follows:

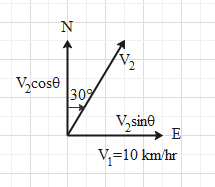
Here we have resolved the velocity ${{\text{v}}_2}$ into its components ${{\text{v}}_2}\sin \theta $ and ${{\text{v}}_2}\cos \theta $ where $\theta = 30^\circ $.

We see that component ${{\text{v}}_2}\sin \theta $ coincides with ${{\text{v}}_1}$ which means that they must be equal to each other. So, we can write

$
  {{\text{v}}_2}\sin \theta = {{\text{v}}_1} \\
   \Rightarrow {{\text{v}}_2} = \dfrac{{{{\text{v}}_1}}}{{\sin \theta }} \\
$

Putting the known values, we get

${{\text{v}}_2} = \dfrac{{10}}{{\sin 30^\circ }} = 10 \times 2 = 20km/h$

This is the required value and the correct answer is option C.

Additional information:
The magnitude of a vector can be calculated from its components using the Pythagoras theorem. If a vector V has components ${{\text{v}}_x}$ and ${{\text{v}}_y}$ then magnitude of vector V is given by the following expression:

${\text{V}} = \sqrt {{\text{v}}_x^2 + {\text{v}}_y^2} $

We can also resolve components of a vector in 3 dimensions. In case of 3-dimensional representation, the components of V would be ${{\text{v}}_x}$, ${{\text{v}}_y}$ and ${{\text{v}}_z}$. The magnitude of V in this case is given by modified Pythagorean Theorem as the following expression:

${\text{V}} = \sqrt {{\text{v}}_x^2 + {\text{v}}_y^2 + {\text{v}}_z^2} $

Note: The components of a vector are constructed using trigonometric identities which satisfy the Pythagorean Theorem for the magnitude of the vector. The components signify the directions in which a part of the main vector can be distributed and we designate those directions to be along the coordinate axes.