Question

A ship is travelling due east at $10\text{ km/h}$. A ship heading ${{30}^{0}}$ east of north, is always due north from the first ship. The speed of the second ship in $\text{km/h}$ is –
$\begin{align}
  & \text{A}\text{. 20}\sqrt{2} \\
 & \text{B}\text{. }\dfrac{20\sqrt{3}}{2} \\
 & \text{C}\text{. 20} \\
 & \text{D}\text{. }\dfrac{20}{\sqrt{2}} \\
\end{align}$

Answer 1

Hint: First draw the diagram according to the question. Then try to break the velocities into their components. Find the relative velocity of the second ship with respect to the first ship. Then you will find the velocity of the second ship.

Complete step by step answer:

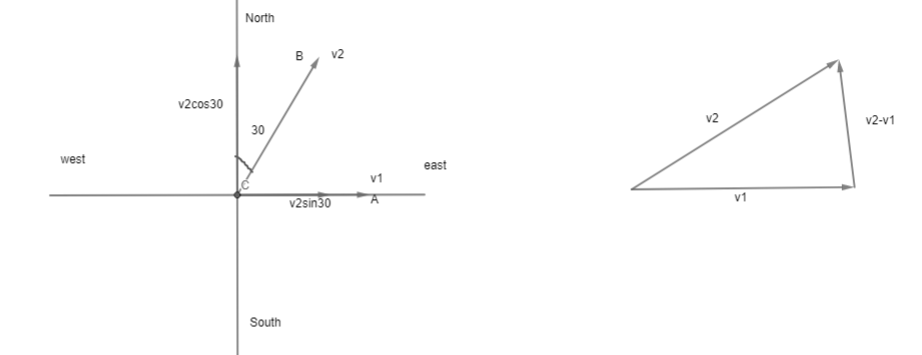
Let the first ship be A and the second ship is B. The first ship is moving with velocity ${{v}_{1}}$ and the second ship moves with velocity with velocity ${{v}_{2}}$.

The second ship is moving in the direction ${{30}^{0}}$ east of north is always. Breaking the velocity of the second ship into components, along the x direction velocity component of second ship will be ${{v}_{2}}\sin {{30}^{0}}$ and in the x direction velocity component will be, ${{v}_{2}}\cos {{30}^{0}}$.

Now, the first ship is moving in the x direction with velocity ${{v}_{1}}$ .

Velocity of the second ship with respect to the first ship will be,

$\begin{align}
  & v={{v}_{2}}-{{v}_{1}} \\
 & v=\left( {{v}_{2}}\sin 30\hat{i}+{{v}_{2}}\cos 30\hat{j} \right)-10\hat{i} \\
 & v=\left( \dfrac{{{v}_{2}}}{2}-10 \right)\hat{i}+\dfrac{\sqrt{3}{{v}_{2}}}{2}\hat{j} \\
\end{align}$

Since, the second ship is always due north of the first ship, the east component of the relative velocity will be zero.

Hence,

$\begin{align}
  & \dfrac{{{v}_{2}}}{2}-10=0 \\
 & {{v}_{2}}=20\text{ }{}^{km}/{}_{h} \\
\end{align}$

The velocity of the second ship is ${{v}_{2}}=20\text{ }{}^{km}/{}_{h}$

The correct option is (C).

Note: In this type of question always try to draw the free body diagram. It will help you solve the question. Relative velocity can be defined as the velocity of an object relative to another object which is assumed to be at rest frame.