Question

A shell of mass \[M\] and radius \[R\] has a point mass \[m\] placed at a distance \[r\] from its centre. The gravitational potential energy \[U(r)\] vs \[r\] will be (assuming \[U(\infty ) = 0\])
A.

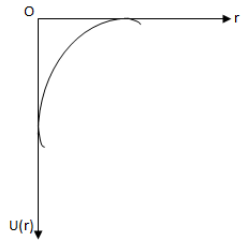
B.

 C.

D.

Answer 1

Hint:We are asked to select the graph for \[U(r)\] vs \[r\]. First recall the formula for gravitational potential energy between two bodies. Write down the possible cases that can be formed using the given information and find the gravitational potential energy for each case. Then plot the graph including all the cases. Observe which option matches with the graph obtained.

Complete step by step answer:
Given, mass of shell is \[M\],Radius of the shell is \[R\],Mass of the point object \[m\],Distance between centre of the shell and the point object is \[r\].And the assumption is made that \[U(\infty ) = 0\].
The formula for gravitational potential energy is written as,
\[U(r) = - \dfrac{{GMm}}{r}\] (i)
where \[G\] is gravitational constant, \[M\] is the mass of the attracting body, \[m\] is the mass the gravitational force is acted upon and \[r\] is the distance between the centers of the bodies

There can be three ways of placing the point object.
(i) When the point object is placed at the surface of the shell that is \[r = R\]. Let us understand with a diagram

Here, the gravitational potential energy will be (using equation (i) and \[r = R\]),
\[U(r = R) = - \dfrac{{GMm}}{R}\] (ii)
(ii) When the point object is inside the shell that is \[r < R\].

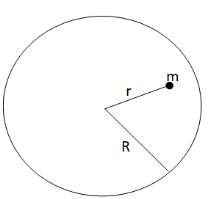
The gravitational potential energy inside a shell is the same as that of the surface of the shell.
So, the gravitational potential energy in this case will be (using equation (ii))
\[U(r < R) = - \dfrac{{GMm}}{R}\] (iii)

(iii) When the point object is outside the shell that is \[r > R\].

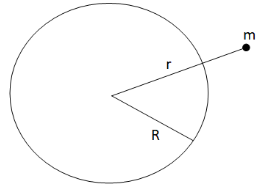
 The gravitational potential energy in this case will be (using equation (i))
\[U(r > R) = - \dfrac{{GMm}}{r}\] (iv)
Now, we draw the graph of \[U(r)\] vs \[r\] for all the above cases.
We observe from equations (ii) and (iii) that for the point object inside the shell and at the surface of the shell, the gravitational potential energy is same that is we can say the gravitational potential energy is constant till the surface, so the graph for case (i) and (ii) will be like

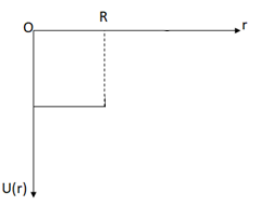
Now, for the third case we observe from equation (iv) that the gravitational potential energy increases with increase in distance \[r\]. So, if we include the third case and the assumption \[U(\infty ) = 0\] in the above graph and we will have the graph as,

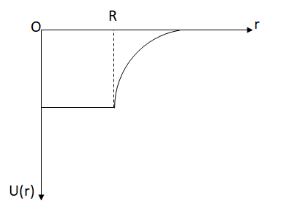
Now, comparing with the options given, the graph matches with the option (3).

Hence, the correct answer is option C.

Note:Gravitational potential energy is the energy stored in an object due to a gravitational field. Always remember that for a shell the potential energy inside the shell is the same as that at the surface, or we can say that gravitational potential energy inside a shell is constant. This point is important for solving many questions, so always try to remember this point.