Question

A shell is fired from a point O on the level ground with velocity $50m/s$ at angle $53{}^\circ $. A hill of uniform slope $37{}^\circ $ starts from point A that is 100m away from the point O as shown in the figure. Calculate the time of flight (in seconds).

Answer 1

Hint: As a first step, you could depict the given information on to a figure. You could then find the total horizontal distance covered (range of projectile) from the sum of distance OA and the horizontal distance covered from A on hitting the hill. Now dividing the horizontal range by the horizontal velocity will give you the time of flight of the given projectile.

Formula used:
Equation of a projectile,
$y=x\tan \theta \left( 1-\dfrac{x}{R} \right)$

Complete step by step solution:
In the question a shell is being fired from point O with velocity $50m/s$ at an angle $53{}^\circ $. We also have a hill of uniform slope of $37{}^\circ $ that starts from point A 100m away from O. We are asked to find the time of flight using the given information. Situation is depicted in the diagram below.

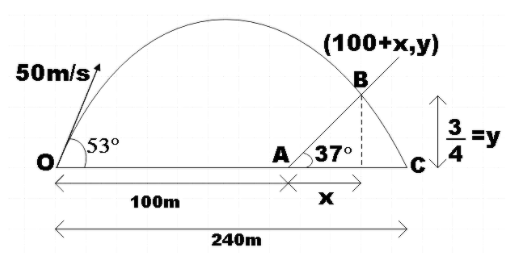
You may recall that the equation of projectile motion is given by,
$y=x\tan \theta -\dfrac{g{{x}^{2}}}{2{{u}^{2}}{{\cos }^{2}}\theta }$
$\Rightarrow y=x\tan \theta \left( 1-\dfrac{gx\cos \theta }{2{{u}^{2}}{{\cos }^{2}}\theta \sin \theta } \right)$
$\therefore y=x\tan \theta \left( 1-\dfrac{x}{R} \right)$ ……………………………………… (1)
The range of the given projectile,
$R=\dfrac{{{u}^{2}}\sin 2\theta }{g}$
$\Rightarrow R=\dfrac{{{50}^{2}}\sin \left( 2\times 53 \right)}{g}$
$\Rightarrow R=\dfrac{2500\times 0.96}{10}$
$\therefore R=240m$
Now let us substitute this in equation of projectile to get,
$y=\left( 100+x \right)\tan 53{}^\circ \left( 1-\dfrac{x+100}{240} \right)$
$\Rightarrow {{x}^{2}}+95x-14000=0$
$\Rightarrow x=\dfrac{-95\pm \sqrt{{{\left( 95 \right)}^{2}}+4\left( 14000 \right)}}{2}$
$\therefore x=80m$
We will get the time of flight by dividing the horizontal distance covered by horizontal velocity.
We know that the horizontal distance covered is given by,
$100+x=100+80=180m$
And the horizontal velocity could be given by,
${{v}_{x}}=u\cos \theta =50\cos 53{}^\circ $
$\therefore {{v}_{x}}\approx 30m/s$
Now we could get time flight as,
${{T}_{f}}=\dfrac{180}{30}=6s$
So we have found the time of flight of the given projectile as 6s.

Note:
Now, if you are curious to find at what distance from point A the shell hits the hill, you could easily find it using the given information. Cosine of the inclination of the hill is given by,
$\cos 37{}^\circ =\dfrac{x}{AB}$
Where, AB is the distance that we want to find.
$AB=\dfrac{80}{\cos 37{}^\circ }=\dfrac{80}{0.75}$
$\therefore AB=100m$