Question

A semicircular thin sheet of metal of diameter 28 cm is bend an open cup conical is made. Find capacity of cup.

Answer 1

Hint: In this question, we need to evaluate the volume of the conical curve such that a semicircular thin sheet of metal of diameter 28 cm is bent and an open cup conical is made. Cone - A cone is a type of geometric shape. They have a flat surface on one side that tapers to a point on the other side.
In order to calculate the surface area and volume of a cone we first need to understand few terms:
Radius, r - The radius is the distance from the center to the edge of the circle at the end.
Height,h - The height is the distance from the center of the circle to the tip of the cone.
Slant height,l - The slant height is the length from the edge of the circle to the tip of the cone.
Let’s understand all the terms with the help of diagrams.

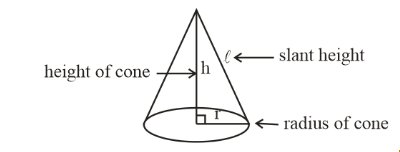
On folding the semicircular sheet, the radius becomes the slant height of the cone.
The circumference of the sheet will be equal to the circumference of the cone.
By using these two relations we can calculate the height and radius of the cone.
Formula used : Volume( capacity) - The volume is how much space takes up the inside of a cone.
Volume of cone \[ = \dfrac{1}{3}\pi {r^2}h\] where r is the radius of the cone and h is the height of the cone.

Complete step by step solution:
According to question:
Diameter of semicircular sheet is$ = $ 28cm
So its radius, \[r = \dfrac{{28}}{2} = 14cm\]
Let’s draw the diagram for the question.

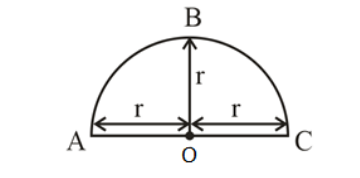
Where we fold it to make a cone it will be like this.

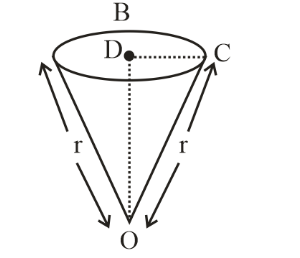
From above diagram $AO = OC = r$ is the radius of a semicircular sheet and after folding it in a cone AO and OC becomes a slant height of the cone.
Let the center of cone be D.
Then DC will become the radius for the cone.
Let the radius of the cone be R.
Now we will find out radius, R of cone.
According to our question cone is made of semi-circle so,
We can write,
Circumference of semicircle$ = $ circumference of cone
Therefore,
 \[\pi r = 2\pi R\]
 \[14 = 2 \times R\]
Or, R $ = $ 7cm
Here
$\pi r$, is the circumference of a semicircle.
$2\pi R$, is the circumference of the base of the cone.
So,
we get radius, R of cone $ = $ 7cm ….. (1)
Now we need the height of the cone.

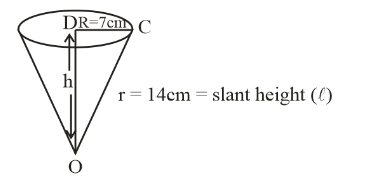
We know that triangle ODC is a right angle triangle so by using Pythagoras theorem we can find out the height of the cone.
${(Hypotenuse)^2} = {(Perpendicular)^2} + {(Base)^2}$
${(OC)^2} = {(OD)^2} + {(DC)^2}$
${(14)^2} = {(h)^2} + {(7)^2}$
${(h)^2} = \sqrt {{{(14)}^2} - {{(7)}^2}} $
$h = \sqrt {147} $or$h = 7\sqrt 3 $
So,
We get height, h of cone \[ = 7\sqrt 3 \] …….(2)
Now we have to calculate the capacity (volume) of the cone.
By using formula and values obtained in equation 1 and 2 we can write,
Volume of cone is calculated as:
 \[
  V = \dfrac{1}{3}\pi {R^2}h \\
   = \dfrac{1}{3} \times \dfrac{{22}}{7} \times {(7)^2} \times 7\sqrt 3 \\
   = 622.38{\text{ c}}{{\text{m}}^3} \;
 \]
So, when a semicircular thin sheet of metal of diameter 28 cm is bent to make an open cup conical its capacity will be \[622.38c{m^3}\] .
So, the correct answer is “ \[622.38c{m^3}\] ”.

Note: Some points are to be remember-
The slant of a right circle cone can be figured out using the Pythagoras Theorem if you have the height and the radius.
Answers for volume problems should always be in cubic units.
Answers for surface area problems should always be in square units.