Question

A semicircular piece of paper of radius \[14\]cm is rolled to form a cone of the largest possible size. Find the capacity of the cone.
A.$721.5{\text{ c}}{{\text{m}}^3}$
B.${\text{645}}{\text{.10 c}}{{\text{m}}^3}$
C.${\text{449}}{\text{.64 c}}{{\text{m}}^3}$
D.${\text{622}}{\text{.37 c}}{{\text{m}}^3}$

Answer 1

Hint: -Here on rolling the paper, radius of the semicircular paper becomes the slant height of the cone and the circumference of the circle is equal to the circumference of the cone. So find the radius of the cone (R). We know that Volume of cone=$\dfrac{1}{3}\pi {R^2}h$. So use this formula to find the volume of the cone.

Complete step-by-step answer:
Given, the radius of semicircular piece of paper r=$14$ cm
It is rolled into the largest possible sized cone. We have to find the capacity of the cone. So we will find the volume of the cone.

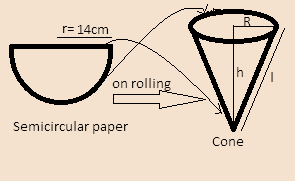
The radius of the semicircular paper becomes the slant height of the cone so if slant height of cone is given by l then $l = 14$cm
And the circumference of the circle is equal to the circumference of the cone as both contain the same part of the paper.
Then we know that circumference of semicircle=$\pi r$
So on putting the values in the formula, we get-
$ \Rightarrow $ Circumference of semicircle=$14\pi $
Now we know that circumference of cone=$2\pi R$
Now, since the circumference of semicircle is equal to the circumference of cone so we get-
$ \Rightarrow 2\pi R = 14\pi $
On solving, we get-
$ \Rightarrow R = 7$ cm
Now we have to find the height of the cone. From the figure we can see that the base of the cone forms a right angle triangle with the slant height of the cone so we can use Pythagoras theorem to find the value of h.
According to the Pythagoras theorem-${H^2} = {P^2} + {B^2}$ Where H is the hypotenuse, P is the perpendicular of the triangle and B is the Base of the triangle
Here R is the base, l is the hypotenuse so and h is the perpendicular.
On putting the values we get-
$ \Rightarrow {l^2} = {R^2} + {h^2}$
On putting the values of R and l, we get-
$ \Rightarrow {14^2} = {7^2} + {h^2}$
On solving, we get-
$ \Rightarrow h = \sqrt {196 - 49} = \sqrt {147} = 7\sqrt 3 $
Now, we know that Volume of cone=$\dfrac{1}{3}\pi {R^2}h$
On putting the values in the formula, we get-
$ \Rightarrow $ Volume of cone=$\dfrac{1}{3} \times \dfrac{{22}}{7} \times 7 \times 7 \times 7\sqrt 3 $
On solving, we get-
$ \Rightarrow $ Volume of cone=$622.37{\text{ c}}{{\text{m}}^3}$
The correct answer is option D.

Note: Pythagoras theorem states that, “In a right angled triangle, the sum of the square of hypotenuse side is equal to the sum of squares of the two other sides.” Hence we write it as-${H^2} = {P^2} + {B^2}$
It is better to draw the diagram of a triangle to understand which is the base of the triangle and which is perpendicular of the triangle.

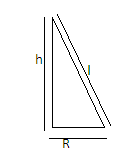
Here it is clear from the diagram that radius is the base and slant height is the hypotenuse.