Question

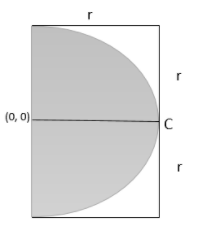
A semicircular disc of radius ‘r’ is removed from a rectangular plate of sides r and 2r. Calculate C.M of remaining portion with respect to origin .

Answer 1

Hint: If we talk about the centre of mass of a body, then this point is dealing with the mass of the whole body. The centre of mass of a body is a point that behaves like the entire mass of the body exists at that point. If we choose a symmetrical body that has a symmetrical mass distribution, then the centre of mass of that body lies exactly at the centre of the body. Like a uniformly shaped pencil of length 10 cm has a centre of mass at 5cm from any end. If a body is heavy at one end, the centre of mass shifts towards the heavy portion. To find the centre of mass in a particular axis we use a formula for two mass systems.

Complete answer:
Position of centre of mass \[=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}\]
Here we have \[{{m}_{1}}{{m}_{2}}\to \]masses of the two particles
And \[{{x}_{1}}{{x}_{2}}\to \] distance at x – axis respectively.
Here we can calculate the remaining area by subtracting the area of semicircle from the area of rectangular plates.
Remaining areas = Area of rectangular plate - Area of semicircles
Now let we define \[\sigma =\] mass per unit area
\[=\dfrac{M}{2{{r}^{2}}}\]
Here M = mass of rectangular slab
Mass of semicircular position \[=\sigma \times \dfrac{\pi {{r}^{2}}}{2}=\dfrac{M\pi }{4}\]
Now let calculate centre of mass of remaining portion = \[=\dfrac{{{m}_{1}}{{r}_{1}}-{{m}_{2}}{{r}_{2}}}{{{m}_{1}}-{{m}_{2}}}\]
Here \[{{m}_{1}}=\]mass of rectangular portion
\[{{m}_{2}}=\] mass of semicircular portion
\[{{r}_{1}}{{r}_{2}}=\] position of centre of mass of rectangular and semicircular portion with respect to O
We have values of \[{{r}_{1}}\] and \[{{r}_{2}}\].
Hence
Centre of mass of remaining portion
\[=\dfrac{\dfrac{Mr}{2}-\left( \dfrac{M\pi }{4} \right)\times \left( \dfrac{4r}{3\pi } \right)}{M-\dfrac{M\pi }{4}}=\dfrac{2r}{3\left( 4-\pi \right)}\]
\[{{x}_{com}}=\dfrac{2r}{3\left( 4-\pi \right)}\]

Note:
Centre of mass of a body as we discussed in the HINT portion can be estimated by the shape and distribution of mass of the body. Sometimes we will find the centre of mass can be outside the body. This is the case for structures like rings and hollow bodies. On flat surfaces, we find a centre of mass on the body.