Question

A self-help group wants to manufacture joker’s caps (conical shapes) of 3 cm radius and 4 cm height. If the available colour paper sheet is 1000 $c{{m}^{2}}$, then how many caps can be manufactured from that paper sheet?

Answer 1

Hint: First, we need to understand that cones are formed by folding papers. The paper required will be equal to the curved surface area of the cone as they are caps and need to be followed and open from below. With the help of the given height and base radius, we will find the slant height of the cone. Once we get the slant height, we can find the curved surface area of the cone given by the relation $S=\pi rl$, where r is the base radius and l is the slant height of the cone. Once we find the used by one cap, we can use a unitary method to find the number of caps that can be manufactured.

Complete step-by-step answer:
It is given to us that the joker’s caps are conical in shape, with the base radius as 3 cm and the height as 4 cm.
The cone will look as follows:

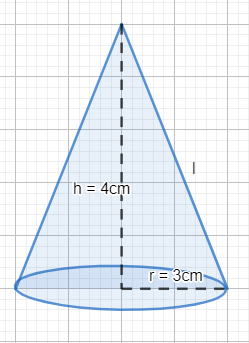
We can see that the height, slant height and the base radius form a right angled triangle. The slant height is the hypotenuse of the triangle.
Thus, we can find the slant height with the help of Pythagoras theorem.
$\begin{align}
  & \Rightarrow {{l}^{2}}={{r}^{2}}+{{h}^{2}} \\
 & \Rightarrow {{l}^{2}}={{\left( 3 \right)}^{2}}+{{\left( 4 \right)}^{2}} \\
 & \Rightarrow {{l}^{2}}=9+16 \\
 & \Rightarrow {{l}^{2}}=25 \\
 & \Rightarrow l=5 \\
\end{align}$
Hence, the slant height of the conical cap is 5 cm.
We know that the curved surface area of a cone is given by the formula $S=\pi rl$.
$\begin{align}
  & \Rightarrow S=\pi \left( 3 \right)\left( 5 \right) \\
 & \Rightarrow S=3.14\left( 15 \right) \\
 & \Rightarrow S=47.12 \\
\end{align}$
Hence, the area of paper required for one cap is 47.12 $c{{m}^{2}}$.
The available area of sheet available with us 1000 $c{{m}^{2}}$. Therefore, we can find the number of caps as the quotient of the total sheet available with us and the area of sheet required for one cap.
$\begin{align}
  & n=\dfrac{1000}{47.12} \\
 & n=21.22 \\
\end{align}$
Therefore, 21 caps can be manufactured.

Note: The unitary method helps us to find the final resources required for something, if we know the resources required for one unit and number of units to be produced. We can tweak this according to our requirement.