Question

A scooterist follows a track on the ground that turns to his left by an angle of \[60{}^\circ \] after every 400m. Starting from the given point displacement of the scooterist at the third and eighth turn are:
A. \[800m;0m\]
B. \[800m;800\sqrt{3}m\]
C. \[800m;400\sqrt{3}m\]
D. \[800;800\sqrt{3}m\]

Answer 1

Hint: If the scooterist turns \[60{}^\circ \] after every 400 m, he will follow the path of a hexagon. To calculate the displacement, we will calculate the shortest distance from the origin to the point where the scooterist took the third turn. The same process will be repeated for the eighth turn.

Complete step-by-step solution:

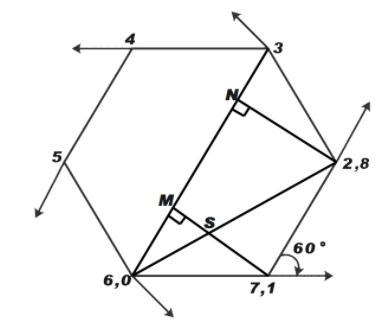
As shown in the figure, the length of line 0-M-N-3 is given by say L
Therefore,
$L = 0M + MN + N3$ …………….. (1)
From the figure, we can say that length 0M is given by
 $ 0M = 400\; \cos 60{}^\circ m $
Similarly, using the trigonometric ratios we can find other lengths
$MN = 400 m$
$\Rightarrow N3 = 400 \; \cos 60{}^\circ m$
Therefore, after substituting the obtained values in equation (1).
We get,
$L = 400\; \cos 60{}^\circ m + 400m + 400\; \cos60{}^\circ m$
Therefore,
$L= (2)(400) m$
$\Rightarrow L = 800 m$
Therefore, the displacement of the scooterist at the third turn is 800 m. ……………. (A)
Similarly, let us find the distance between 0-8.
Therefore,
$0-8 = 0S + S8$ …………….. (2)
In the figure, the angle at point 1 made by line 0-1-2 is 120 degrees. Now, the two sides of the hexagon are equal. Therefore, by property of the isosceles triangle, the remaining angle can be given as 30 degrees.
Therefore,
$0-8 = 400\; \cos 30{}^\circ + 400\; \cos 30{}^\circ $
\[\Rightarrow 0-8 = 2\times (400\times \dfrac{\sqrt{3}}{2})\]
\[\Rightarrow 0-8 = 800 \sqrt{3}\] m
Therefore, displacement of the scooter at the eighth turn is 800\[\sqrt{3}\] m. ……………..(B)
From (A) and (B),
The correct answer is option D.

Note: Displacement is defined as the shortest distance between the initial point and the final point. Displacement is independent of the path. It is a vector quantity that means it has magnitude as well as direction. We have not been asked the direction in this question.