Question

A school provides milk to the students daily in cylindrical glasses of radius k cm. If the glass is filled with milk up to height 12 cm, then the litres of milk needed to serve 1600 students is 73.92l. Find the value of 2k.

Answer 1

Hint: From the question, it was given that a school provides milk to the students daily in cylindrical glasses of radius k cm. We were also given that a glass is filled with milk up to height 12 cm. We were also given that 1600 students are served with 73.92 l. Now we have to find the volume of the cylinder whose radius is equal to k cm and height of cylinder is equal to 12 cm. We know that the volume of the cylinder is equal to \[\pi {{r}^{2}}h\] where “r” is the radius of the cylinder and “h” is the height of the cylinder. By using this formula, we can find the value of volume in terms of k. It was given that the volume of 1600 glasses is equal to 73.92l. We know that 1 litre is equal to 1000 cubic centimetres. Now we will find the volume of 73.92 l in cubic centimetre. Now we will equate the volume obtained in terms of k and the volume of 73.92 l in cubic centimetre. Now by solving we will get the value of k. Now we will find the value of 2k.

Complete step-by-step answer:
Before solving the question, we should know that the volume of the cylinder is equal to \[\pi {{r}^{2}}h\] where “r” is radius of cylinder and “h” is height of cylinder.
From the question, it was given that a school provides milk to the students daily in cylindrical glasses of radius k cm. We were also given that a glass is filled with milk up to height 12 cm. We were also given that 1600 students are served with 73.92 l.

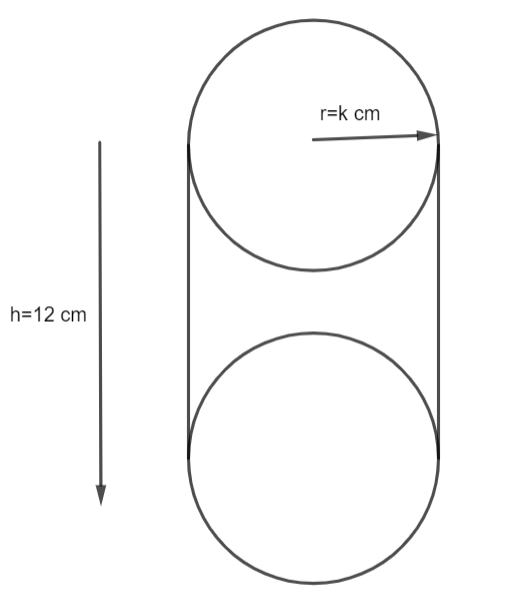
Now we have to find the volume of the cylinder whose radius is equal to k cm and height of cylinder is equal to 12 cm.
So, we get
the volume of cylinder \[=\pi {{\left( k \right)}^{2}}\left( 12 \right)=12\pi {{k}^{2}}\]
It was given that a glass is in the shape of a cylinder.
It was also given that 1600 students have 1600 glasses.
So, we have to calculate the volume of 1600 glasses.
So, we get
Volume of 1600 glasses \[=1600(12\pi {{k}^{2}})=\left( 192\pi {{k}^{2}} \right){{10}^{2}}c{{m}^{3}}\]
It was given that the volume of 1600 glasses are equal to 73.92l.
We know that 1 litre is equal to 1000 cubic centimetres.
So, the volume of 1600 glasses are equal to \[739.2\times {{10}^{3}}c{{m}^{3}}\].
So, we get
\[\Rightarrow \left( 192\pi {{k}^{2}} \right){{10}^{2}}=739.2\times {{10}^{3}}\]
By cross multiplication, we get
\[\begin{align}
  & \Rightarrow {{k}^{2}}=\dfrac{739.2\times {{10}^{3}}}{192\pi \times {{10}^{2}}} \\
 & \Rightarrow {{k}^{2}}=\dfrac{7392}{192\pi } \\
 & \Rightarrow {{k}^{2}}=\dfrac{7392\times 7}{192\times 22} \\
 & \Rightarrow {{k}^{2}}=12.25 \\
 & \Rightarrow k=3.5....(1) \\
\end{align}\]
From equation (1), it is clear that the value of k is equal to 3.5.
Now we have to calculate the value of 2k.
\[\begin{align}
  & \Rightarrow 2k=2(3.5) \\
 & \Rightarrow 2k=7......(2) \\
\end{align}\]
From equation (2), it is clear that the value of 2k is equal to 7.

Note: Students may have a misconception that 1 litre is equal to 1000 cubic metre. Then we get 1 litre is equal to \[{{10}^{6}}\] cubic centimetre. Then we get
The volume of 1600 glasses is equal to \[739.2\times {{10}^{6}}c{{m}^{3}}\].
So, we get
\[\Rightarrow \left( 192\pi {{k}^{2}} \right){{10}^{2}}=739.2\times {{10}^{6}}\]
By cross multiplication, we get
\[\begin{align}
  & \Rightarrow {{k}^{2}}=\dfrac{739.2\times {{10}^{6}}}{192\pi \times {{10}^{2}}} \\
 & \Rightarrow {{k}^{2}}=\dfrac{7392}{192\pi }\times {{10}^{4}} \\
 & \Rightarrow {{k}^{2}}=\dfrac{7392\times 7}{192\times 22}\times {{10}^{4}} \\
 & \Rightarrow {{k}^{2}}=1225 \\
 & \Rightarrow k=35....(1) \\
\end{align}\]
From equation (1), it is clear that the value of k is equal to 35.
Now we have to calculate the value of 2k.
\[\begin{align}
  & \Rightarrow 2k=2(35) \\
 & \Rightarrow 2k=70......(2) \\
\end{align}\]
From equation (2), it is clear that the value of 2k is equal to 70.
But we know that the value of 2k is equal to 7, so we have to avoid this misconception to have a correct answer.