Question

A school auditorium is 40m long, 30m broad and 12m high. If each student requires 1.2 sq m of the floor area, find the maximum number of students who can be accommodated in this auditorium.
(a) 790
(b) 980
(c) 1000
(d) 1110

Answer 1

Hint: It is given in the question that each student requires 1.2 sq m of the floor area. Also, it is given that the dimensions of the cuboidal auditorium is 40m long, 30m broad and 12m high. So, to find the answer, find the area of the floor by multiplying the length and breadth of the cuboid and divide the result by the area required by each student.

Complete step-by-step answer:
Let us start by drawing a representative diagram of the situation given in the question for better understanding.

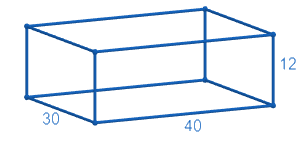
Let us start by finding the area of the floor of the cuboidal auditorium. We know that the base of a cuboid is a rectangle and the area of a rectangle is the product of its length and breadth. For the given auditorium, the length of the base is 40m and the breadth of the base is 30m.
$\text{Area of the floor}=l\times b=40\times 30=1200{{m}^{2}}$ .
Now it is given that each student requires a 1.2 sq m of area on the floor for standing at the auditorium. So, the total number of students who can be in the auditorium is the total area of the floor divided by the area of the floor used by each student.
$\therefore \text{Total number of students}=\dfrac{1200}{1.2}=1000$
Therefore, we can conclude that the answer to the above question is option (c).

Note: Don’t get confused and consider the total surface area of the cuboidal auditorium as the available area and divide the total surface area by area occupied by each student, as a person can stand only on the floor and humans are not capable of standing on the walls or ceiling of the auditorium without any support.