Question

A satellite of the moon revolves around it in radius n times the radius of the moon (R). Due to cosmic dust,it experiences a resistance $f = a{v^2}$. Find how long it will stay in the orbit.
(a). $\dfrac{m}{{a\sqrt {\dfrac{{GM}}{R}} }}\sqrt n $
(b). $\dfrac{m}{a}\sqrt {\dfrac{R}{{GM}}} \left( {\sqrt n - 1} \right)$
(c). $\dfrac{m}{a}\dfrac{{\left( {\sqrt n - 1} \right)}}{v}$
(d). $\dfrac{m}{a}\dfrac{{{v_l}}}{{v_f^2}}$

Answer 1

- Hint: In this question, we first find the force due to air resistance as $f = \dfrac{{aGM}}{r}$ by using $v = \sqrt {\dfrac{{GM}}{r}} $ then we find word done using $dw = fvdt$ that is \[dw = a{\left( {\dfrac{{GM}}{r}} \right)^{\dfrac{3}{2}}}dt\] . After that we find the total energy as $E = - \dfrac{{GMm}}{{2r}}$ then we use the work energy theorem that is $dw = - dE$

Complete step-by-step solution -

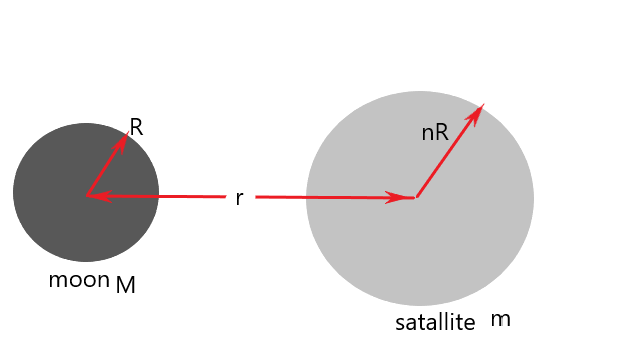
Here it is given that the resistance due to the cosmic dust is
 \[f = a{v^2}\]---------------------- (1)
Where $v$ is the velocity of the satellite and it is given as
$v = \sqrt {\dfrac{{GM}}{r}} $---------------------- (2)
Here G is the universal gravitational constant
          M is the mass of the moon
And r is the distance of the satellite from the moon
Now substituting equation (2) in equation (1) we get
$f = a{\left( {\sqrt {\dfrac{{GM}}{r}} } \right)^2}$
$ \Rightarrow f = \dfrac{{aGM}}{r}$---------------------- (3)
Now we will find the small work done $dw$ by the force $f$ of cosmic dust resistances that is
 $dw = fdx$
 We can replace $dx = vdt$because velocity can be written as $v = \dfrac{{dx}}{{dt}}$ , so we will get
$dw = fvdt$-------------------- (4)
Now substituting equation (2) and equation (3) in equation (4) we get
$dw = \left( {\dfrac{{aGM}}{r}} \right)\left( {\sqrt {\dfrac{{GM}}{r}} } \right)dt$
\[ \Rightarrow dw = a{\left( {\dfrac{{GM}}{r}} \right)^{\dfrac{3}{2}}}dt\]-------------------------- (5)
We know that the total energy is sum of potential and kinetic energy
Here kinetic energy is given as
$\dfrac{1}{2}m{v^2}$
Putting $v = \sqrt {\dfrac{{GM}}{r}} $in this we get
$KE = \dfrac{{GMm}}{{2r}}$
Here potential energy is given as
$PE = - \dfrac{{GMm}}{r}$
So, total energy is given as
$E = PE + KE$
$ \Rightarrow E = - \dfrac{{GMm}}{r} + \dfrac{{GMm}}{{2r}}$
$ \Rightarrow E = - \dfrac{{GMm}}{{2r}}$------------------------------- (6)
Now we find the change in energy that is
$ \Rightarrow dE = - d\left( {\dfrac{{GMm}}{{2r}}} \right)$
\[ \Rightarrow dE = - \left( { - \dfrac{{GMm}}{{2{r^2}}}} \right)\]
\[ \Rightarrow dE = \dfrac{{GMm}}{{2{r^2}}}\]-------------------------------- (7)
Now by applying the work energy theorem that the change in energy is equal to the word done, $dw = - dE$------------------------------------- (8)
Now substituting equation (5) and (7) in (8) we get
$ \Rightarrow - a{\left( {\dfrac{{GM}}{r}} \right)^{\dfrac{3}{2}}}dt = - \dfrac{{GMm}}{{2{r^2}}}$
$ \Rightarrow \left( { - \dfrac{{aGM}}{r}} \right)\left( {\sqrt {\dfrac{{GM}}{r}} } \right)dt = - \dfrac{{GMm}}{{2{r^2}}}$

Now canceling G, M on both side and taking r on one side and then taking integration on both side we get
$ \Rightarrow \dfrac{a}{m}\int_0^t {dt} = \dfrac{1}{2}\sqrt {\dfrac{1}{{GM}}} \int\limits_{ri}^{rf} {{r^{\dfrac{{ - 1}}{2}}}} dr$
$ \Rightarrow \dfrac{a}{m}\int_0^t {dt} = - \dfrac{1}{2}\sqrt {\dfrac{1}{{GM}}} \int\limits_{nR}^R {{r^{\dfrac{{ - 1}}{2}}}} dr$
Now by solving this we get
\[t = \dfrac{m}{a}\sqrt {\dfrac{R}{{GM}}} \left( {\sqrt n - 1} \right)\]
Hence, option B is correct.

Note: For these types of questions we need to be familiar with the concepts of binding energy and satellites, orbital velocity, the minimum distance of approach, the expression for energy for satellites, the expression for the velocity of a satellite orbiting, and gravitational potential energy.