Question

A satellite is orbiting around the earth in an orbit in equatorial plane of radius $2{{R}_{e}}$ (where ${{R}_{e}}$ is the radius of the earth). Find the area on the Earth that this satellite covers for communication purposes in its complete revolution.
A. $4\pi {{R}_{e}}^{2}$
B. $2\pi \sqrt{3}{{R}_{e}}^{2}$
C. $2\pi \left( 2-\sqrt{3} \right){{R}_{e}}^{2}$
D. $2\pi \left( 4+\sqrt{3} \right){{R}_{e}}^{2}$

Answer 1

Hint: On making a neat diagram of the situation given, you will see that there are two patches at north as well as south end that are not covered by the satellite. So, we could simply subtract this area from the total area of Earth to find the answer. You could use the solid angle subtended by these patches at the earth’s center to find the area of the patches.
Formula used:
Solid angle,
$\Omega =2\pi \left( 1-\cos \theta \right)$

Complete answer:
In the question, we are said that a satellite is orbiting around the earth in orbit that is double the Earth’s radius. We are supposed to find the area on the Earth that the satellite covers in one complete revolution for communication purposes.

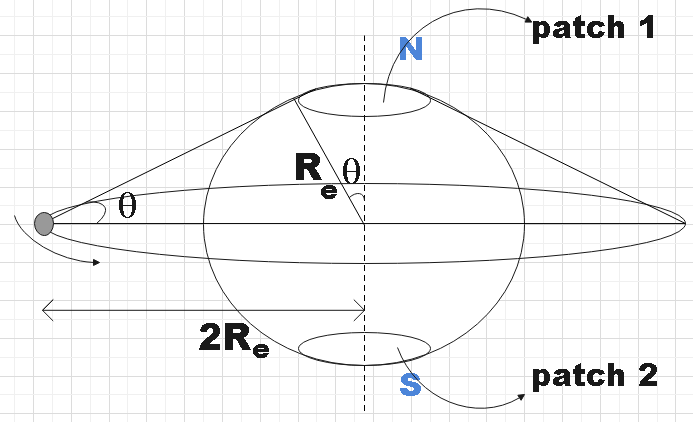
Clearly, we see that there are two patches that are left uncovered by the satellite during its revolution around earth. So, we have to subtract this area from the earth’s total area to get the answer.
We see that,
$\sin \theta =\dfrac{{{R}_{e}}}{2{{R}_{e}}}=\dfrac{1}{2}$
$\Rightarrow \theta =\dfrac{\pi }{6}$ ………………………………………….. (1)
Now, we could find the solid angle subtended by a patch on Earth’s centre as,
$\Omega =2\pi \left( 1-\cos \theta \right)$
$\Rightarrow \Omega =\pi \left( 2-\sqrt{3} \right)steradian$
Now area of a patch would be,
${{A}_{p}}=\Omega {{R}_{e}}^{2}=\pi \left( 2-\sqrt{3} \right){{R}_{e}}^{2}$ ………………………………… (2)
Now, the required area could be given by,
${{A}_{C}}=4\pi {{R}_{e}}^{2}-2{{A}_{p}}$
$\Rightarrow {{A}_{C}}=4\pi {{R}_{e}}^{2}-2\pi \left( 2-\sqrt{3} \right){{R}_{e}}^{2}$
$\therefore {{A}_{C}}=2\sqrt{3}\pi {{R}_{e}}^{2}$
Therefore, we found the area of the earth covered by the satellite for communication purpose to be,
${{A}_{C}}=2\sqrt{3}\pi {{R}_{e}}^{2}$

Option B is correct.

Note:
Solid angle by definition is the measure of the amount of the field of view from a certain point that an object under consideration covers. In other words, we could define it as the measure of how large a particular object appears when viewed from that point. It is normally represented by Greek letter $\Omega $.