Question

A satellite is launched into a circular orbit of radius R around the earth. A second satellite is launched into an orbit of radius 1.01R. The period of the second satellite is larger than the first one by approximately.
A. 0.5%
B. 1.0%
C. 1.5%
D. 3.0%

Answer 1

Hint: The time period of a satellite refers to the time that it takes to make one full orbit around any object. For example, the time period of the Earth to make one full orbit around the sun is one year. You can easily figure out the time period if the satellite's speed as well as the radius at which it orbits, are known. To solve the given problem, we will calculate the period of the first and second satellite from the given data.

Complete step by step answer:
According to the question one satellite is a launch around the earth with the radius R.Another satellite is launched into an orbit of radius 1.01R. First satellite covered total distance is 2R (radius of earth R+ radius of first satellite R is equal to 2R). Second satellite covered total distance is 2.02R (radius of earth R+ radius of first satellite R is equal to 1R + 1.02R radius of second satellite). Refer to the below diagram (self made) for better understanding:

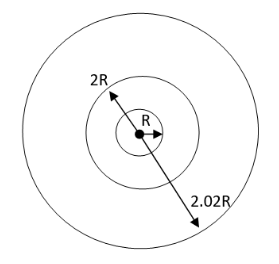
To find out the time period of the second satellite is larger than the first one. We calculate time difference: by $\dfrac{{{T_2} - {T_1}}}{{{T_2}}} \times 100\% $ (y)
As we know that time period of satellite is given by the following formula:
$T = 2\pi \sqrt {\dfrac{{{{\left( {R + H} \right)}^3}}}{{2{R^2}}}} $ (i)
Here, R is the radius of earth, H is the height.
For first satellite H is R, Putting the value of H in equation (i) we get
$
{T_1} = 2\pi \sqrt {\dfrac{{{{\left( {R + R} \right)}^3}}}{{2{R^2}}}} \\
\Rightarrow {T_1} = 2\pi \sqrt {\dfrac{{{{\left( {2R} \right)}^3}}}{{2{R^2}}}} \\
\Rightarrow {T_1} = k\sqrt {{{\left( {2R} \right)}^3}} where\left( {k = 2\pi \sqrt {\dfrac{1}{{2{R^2}}}} } \right)\left( {ii} \right) \\
\Rightarrow{T_2} = 2\pi \sqrt {\dfrac{{{{\left( {R + H} \right)}^3}}}{{2{R^2}}}} \\
$
After putting the value H (2.01R) we get
${T_2} = k\sqrt {{{\left( {2.01R} \right)}^3}} $ (iii)
Putting the equation (ii) and (iii) in (y) we get
$\dfrac{{{T_2} - {T_1}}}{{{T_2}}} \times 100\% $
$\Rightarrow\dfrac{{k\sqrt {{{\left( {2.01R} \right)}^3}} - k\sqrt {{{\left( {2R} \right)}^3}} }}{{k\sqrt {{{\left( {2.01R} \right)}^3}} }} \times 100\% $
$\therefore 1.5\%$

Therefore, the second satellite is 1.5% larger than the first one. Thus, the correct answer is option C.

Note: This is how the time formula derived from T = (circumference of circular orbit)/ (orbital velocity)
$
T = \dfrac{{2\pi r}}{{{v_3}}} \\
\Rightarrow T = \dfrac{{2\pi \left( {R + H} \right)}}{{{v_3}}} \\
\Rightarrow {v_3} = \sqrt {\dfrac{{GM}}{{R + H}}} \\
\Rightarrow GM = g{R^2} \\ $
Put the value GM in vs we get
$
{v_3} = \sqrt {\dfrac{{g{R^2}}}{{R + H}}} \\
\Rightarrow T = \dfrac{{2\pi \left( {R + H} \right)}}{{\sqrt {\dfrac{{g{R^2}}}{{R + H}}} }} \\
\Rightarrow T = 2\pi \sqrt {\dfrac{{{{\left( {R + H} \right)}^3}}}{{2{R^2}}}} $