Question

A running track of 440 ft. is laid out enclosing a football field, the shape of which is rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum, find the length of its longest sides.

Answer 1

Hint- First find out the total perimeter of the football field including the semi-circle and rectangle, and then proceed further and solve it by finding out the area of the rectangular field.

Complete step-by-step answer:

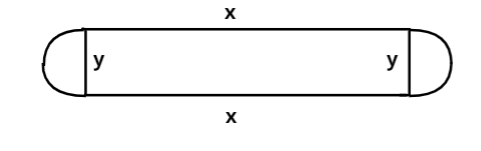
Let us consider the length of the rectangle =x
Let the breadth of the rectangle =y
The perimeter of a rectangle is given by the formula 2x+2y
But here, we have two semi circles also present, as we know the perimeter of a semi-circle is $\pi r$.
Here the radius of the semi-circle is $\dfrac{y}{2}$(Since, breadth is y).
So, we can write the perimeter=$2x + \pi \left( {\dfrac{y}{2}} \right) + \pi \left( {\dfrac{y}{2}} \right)$
                                                         =2x+$\pi y$ =440(Since the total perimeter of the running track is 440ft)
From this, we can write $y = \dfrac{{440 - 2x}}{\pi }$
But, we know that the area of the rectangle is given by
Area= x. y
We already have the value of y, let’s multiply this with x, so we get
Area=$x\left( {\dfrac{{440 - 2x}}{\pi }} \right) = \dfrac{{440x - 2{x^2}}}{\pi }$ .
Now, we need to maximize the portion, so we need to differentiate the area i.e.., $\dfrac{{dA}}{{dx}} = 0$ (Condition for maxima).

On differentiating this with respect to x, we get
$
   \Rightarrow \dfrac{d}{{dx}}\left( {\dfrac{{440x - 2{x^2}}}{\pi }} \right) = 0 \\
   \Rightarrow \dfrac{1}{\pi }\left( {440 - 4x} \right) = 0 \\
   \Rightarrow 440 - 4x = 0 \\
 $
From this, we get
$
  440 = 4x \\
  x = \dfrac{{440}}{4} = 110 \\
 $
Let us substitute the value of x in y we get
$
  y = \dfrac{{440 - 2(110)}}{{\dfrac{{22}}{7}}}\left( {\because \pi = \dfrac{{22}}{7}} \right) \\
  y = \dfrac{{7(220)}}{{22}} = 7(10) = 70 \\
 $
Therefore, x is 110 ft. and y is 70 ft. i.e.., radius of semi-circle is 35 ft.
So, from this, we can say that the length of the rectangular field=110ft.

Note: When solving questions of these types, if we get to maximize or minimize any portion apply differentiation conditions to find the values.