Question

A Rubber stopper on the end of the string is swung steadily in a horizontal circle. In one trial, it moves at speed $v$ in a circle of radius $r$. In a second trial, it moves at a higher speed $3v$ in a circle of radius $3r$. In this second trial, its acceleration is:
A. The same as in the first trial
B. Three times larger
C. One third as large
D. Nine times larger
E. One-ninth large

Answer 1

Hint:The above mentioned question is related to the circular motion of an object. Circular motion of any object gives rise to a force called centripetal force. Here we are supposed to find acceleration when radius and velocity is given and hence we find the relation between them.

Complete step by step answer:
Consider an object moving in a circular path as shown in the figure below.

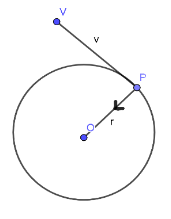
We see that the objects moving in a circular path undergo continuous acceleration at every position because they keep changing their direction. As the body is constantly accelerating we know by Newton’s laws that a force must act on it. This force acting on the object is perpendicular to the direction of motion at every point and is called centripetal force.

Hence
Trial 1:-It is given that speed is v m/s
And radius is r meter.
Trial 2:- It is given that speed =3v
And radius is 3r meter
Like discussed above for a circular motion: F(centripetal) \[ = m \times a\]
\[ \Rightarrow \]\[\dfrac{{m{v^2}}}{r} = m \times a\]
\[ \Rightarrow \]\[a = \dfrac{{{v^2}}}{r}\]
Hence making individual cases for trial 1 and trial2 :

Case 1 : TRIAL 1
Acceleration in the 1st trial will be \[{a_1} = \dfrac{{{v^2}}}{r}\] ------------(1)
Case 2 : TRIAL 2
Acceleration in the 2nd case will be \[{a_2} = \dfrac{{\left( {3{v^2}} \right)}}{{3r}}\]
\[ \Rightarrow \] \[{a_2} = \left( {\dfrac{{9{v^2}}}{{3v}}} \right)\]
\[ \Rightarrow \] \[{a_2} = \dfrac{{3{v^2}}}{r}\]
\[ \therefore \] \[{a_2} = 3{a_1}\] -------------(using equation 1)
Hence we see that acceleration in the 2nd trial is 3 times the acceleration in the first trail.

Hence correct answer is option B.

Note: Remember that circular motion takes place only when force on object is perpendicular to motion of object and acts inwards(towards the centre of the circle). It doesn’t mean that centripetal force is a separate force.