Question

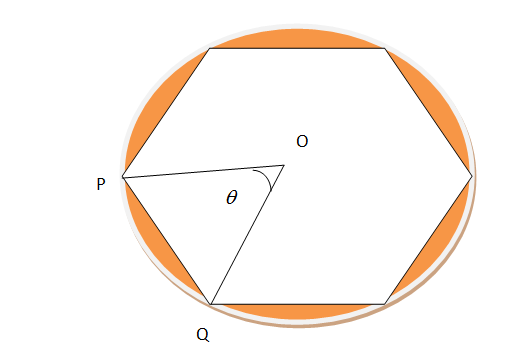
A round table cover has six equal designs as shown in figure. If the radius of the cover is 28 cm, find the cost of making the design at the rate of Rs 3.50 per $cm^2$. (use $\sqrt 3 $ =1.7)

1) Rs 1145.3
2) Rs 1348
3) Rs 1626.8
4) Rs 1723.5

Answer 1

Hint: The above problem is based on the sector area of the circular region and the area of the triangle, which will give the area of the yellow design shown in the figure above.
Area of the sector is given is $\dfrac{\theta }{{{{360}^0}}} \times \pi \times {r^2}$ ($\theta $ is the angle which sector makes an angle which the sector makes with the centre).
Area of the equilateral triangle is given by $\dfrac{{\sqrt 3 }}{4}{a^2}$(a is the side of the equilateral triangle).

Complete step-by-step answer:
Now first of all we will find out the angle theta and then proceed for the problem further.
$ \Rightarrow \theta = \dfrac{{{{360}^0}}}{6}$
$ \Rightarrow \theta = {60^0}$
Area of the sector is given as;
$ \Rightarrow \dfrac{\theta }{{{{360}^0}}} \times \pi {r^2}$
On substituting the value of radius and angle theta in the above formula;
$ \Rightarrow \dfrac{{60}}{{{{360}^0}}} \times \pi {(28)^2}$
$ \Rightarrow \dfrac{{\pi {{(28)}^2}}}{6}$
$ \Rightarrow 410.5014$ $cm^2$
In the figure drawn above there is one triangle named OPQ, If we draw the perpendicular OM of the triangle OPQ.
We will use the concept of Congruent triangles in order to prove two triangles as congruent.
In $\Delta OPM$ and $\Delta OQM$
$\angle M = \angle M({90^0}each)$
$OP = OQ$ (radius of circle)
$OM = OM$ (common)
$\Delta OPM \cong \Delta OQM$
Therefore, $PM = QM$ (corresponding part of congruent triangle)
Now, we can calculate the area of the triangle OPQ which we call an equilateral triangle because all three sides are equal.
Thus area of the triangle is given as;
$ \Rightarrow \dfrac{{\sqrt 3 }}{4} \times 28 \times 28$ (side of the triangle is radius of the circle 28cm)
$ \Rightarrow 196\sqrt 3 $
$ \Rightarrow 339.34$ $cm^2$
Area of the design = area of the sector - area of the triangle
$ \Rightarrow 410.50 - 339.34$
$ \Rightarrow 77.47c{m^2}$
As the design is hexagon, then it has 6 sides,
$ \Rightarrow 6 \times 77.47$
$ \Rightarrow 464.82$
Cost of per $cm^2$ = 3.50Rs
Therefore, total cost of the design is;
$ \Rightarrow 3.50 \times 464.82$
$ \Rightarrow 1626.87$ Rs

Thus, option 3 is correct.

Note:
In the above problem we would have found the area of the triangle by calculating the area of the triangles individually separated by the perpendicular OM by applying the formula of $\dfrac{1}{2} \times b \times h$ (b is the base and h is the height) to each triangle OPM and OQM separately.