Question

A rope thrown over a pulley has a ladder with a man at one of its ends and a counter balancing mass $M$ at its other end. The man whose mass is $m$, climbs upwards by $\Delta r$ relative to the ladder and then stops. Ignoring the masses of the pulley and the rope as well as the friction in the pulley axis, find the displacement of the centre of mass of this system.

Answer 1

Hint: The system is made of the ladder, pulley, man and block. The mass of ladder and pulley are negligible while the masses of man and block are $\text{m}\,\text{and}\,\text{M}$ respectively. Due to displacement of man relative to the ladder, the mass distribution of the system changes so, the position of centre of mass also changes. The difference in the initial and final position of centre of mass is its displacement.

Formulas used:
${{X}_{cm}}=\dfrac{m{{r}_{1}}+M{{r}_{2}}}{m+M}$
$\Delta X=X_{cm}^{'}-{{X}_{cm}}$

Complete answer:

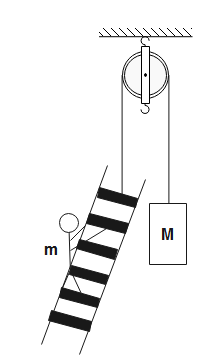
The centre of mass is a hypothetical point at which the whole mass of the system is assumed to be concentrated to make the calculations more simplified.
In the figure, the system of man of mass $m$ on a ladder and a block of mass $M$ are connected to a rope over a pulley.
The initial centre of mass of the system will be-
${{X}_{cm}}=\dfrac{m{{r}_{1}}+M{{r}_{2}}}{m+M}$ ---- (1)
Given that the man moves by a distance $\Delta r$ up the ladder but there will be no change in the position of block. Therefore, the final position of the centre of mass will be-
$X_{cm}^{'}=\dfrac{mr_{1}^{'}+M{{r}_{2}}}{m+M}$ --- - (2)
The change in the position of the centre of mass will be-
$\Delta X=X_{cm}^{'}-{{X}_{cm}}$
Substituting from eq (1) and eq (2) in the above equation, we get,
$\begin{align}
  & \Delta X=\dfrac{mr_{1}^{'}+M{{r}_{2}}}{m+M}-\left( \dfrac{m{{r}_{1}}+M{{r}_{2}}}{m+M} \right) \\
 & \Delta X=\dfrac{mr_{1}^{'}-m{{r}_{1}}}{m+M} \\
 & \Delta X=\dfrac{m(r_{1}^{'}-{{r}_{1}})}{m+M} \\
\end{align}$
We know that
$\Delta r=r_{1}^{'}-{{r}_{1}}$
$\therefore \Delta X=\dfrac{m\Delta r}{m+M}$

Therefore, the centre of mass of the man, ladder and block system gets displaced by $\dfrac{m\Delta r}{m+M}$.

Note:
As the ladder and block are at rest, the motion of the man changes the mass distribution of the system due to which the centre of mass also changes. The system is isolated as there are no external forces acting on it. The motion of the centre of mass is equivalent to the motion of the whole system.