Question

A room 8 m long, 6 m broad and 3 m high has two windows \[1\dfrac{1}{2}\text{m}\times 1\text{m}\] and door $2\text{m}\times \dfrac{1}{2}\text{m}$. Find the cost of papering the walls with paper 50 cm wide at 25p per meter.
A) Rs. 40
B) Rs. 36
C) Rs. 44
D) Rs. 33

Answer 1

Hint: In this question, we need to find the area of the walls, with the help of the formula area of a rectangle = l x b, as there are two pairs of similar walls the formula will change to 2(l x b). Subtract the area of windows and door from the area of the walls. Divide the total area required for papering by the width of the paper to find how many meters of paper will be required. Use that value to calculate the total cost of papering.

Complete step-by-step answer:
Here, a room with the measurements, 8m long, 6m broad and 3m high is given, with windows of $1\dfrac{1}{2}\text{m}\times 1\text{m}$ and door of $2\text{m}\times \dfrac{1}{2}\text{m}$. Let us draw a figure to understand the perspective of the room.

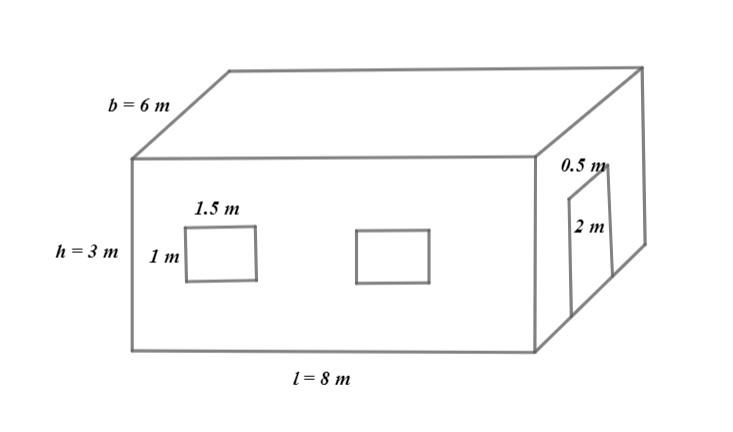
First let us find the area of the walls to be covered, it is obvious that windows and doors won’t be covered. So, subtract the area of the windows and the door from the area of all the 4 walls.
Area of the 4 walls = 2(area of the greater wall) + 2(area of the smaller wall)
                                  = 2(8 x 3) + 2(6 x 3)
                                  = 2(24) + 2(18)
                                  = 48 + 36
                                  $=84{{\text{m}}^{2}}$

Now, let us calculate the area of the windows, because there are two windows of the same size, multiply the area of the single window by 2.
Area of the windows = 2 x (area of the single window)
                                     $\begin{align}
  & =2\times \left( 1\dfrac{1}{2}\times 1 \right) \\
 & =2\times \left( \dfrac{3}{2} \right) \\
 & =3{{\text{m}}^{2}} \\
\end{align}$
Area of the door = length of the door x breadth of the door
                               $\begin{align}
  & =2\times \dfrac{1}{2} \\
 & =1{{\text{m}}^{2}} \\
\end{align}$
Now, subtract the area of the windows and door from the area of all the four walls.
We get, Area required for papering of the walls = 84 – (3 + 1)
                                                                                      = 84 – 4
                                                                                      = 80
Therefore, the area of the room to be covered by the paper is $80{{\text{m}}^{2}}$.
We have been given that a paper of 50cm is used for papering the walls,

Now, we need to find out how much paper is required to cover the walls, here we have to convert
$\begin{align}
  & \dfrac{80}{0.5}=\dfrac{80}{5}\times 10 \\
 & =80\times 2 \\
 & =160\text{m} \\
\end{align}$
The given cost price for the paper used to cover the walls is 25p per meter, let us find the total cost for papering all the 4 walls. Let us consider the total cost to be ‘x’.
$160 = x$
$x = 25 \times 160$
   = 4000
Let us convert the total cost in paise to rupees,
We know that, 1 rupee = 100 paise
Total cost in rupees for papering the walls $=\dfrac{4000}{100}$
                                                                               = 40
Hence, the total cost for papering the walls is Rs. 40.

Note:
Here in this question, we should not find the volume even though we have a cuboid because the volume indicates the space the object occupies but here, we have to find the area of two pairs of similar walls. The measurements of the windows are given in improper fraction, change that into proper fraction and then proceed with the problem.