Question

A room $5.49m$ long and $3.87m$ broad is to be paved with square tiles. Find the edge of the longest tile which will exactly fit.

Answer 1

Hint:As the H.C.F. is the highest common factor, in this question to evaluate the edge of the longest tile, evaluate the H.C.F. of the length and breadth of the rectangle.

Complete step-by-step answer:
We are given that a room $5.49m$ long and $3.87m$ broad is to be paved with square tiles.
The shape of the tiles is square. Therefore, all edges are equal.
We have to evaluate the edge of the longest tile which will exactly fit.
We know that to evaluate the maximum of any two-common numbers, we evaluate their H.C.F. (Highest common factor).
Here, we also evaluate the H.C.F. of the given side lengths.
It is difficult to evaluate the H.C.F. of decimal numbers, so we change the units into $cm$.
We know that $1m = 100cm$
The length of the room will be $5.49 \times 100 = 549cm$
The breadth of the room will be $3.87 \times 100 = 387cm$
Now, we evaluate the H.C.F. of $549$ and $387$ by the prime factorization method.
Write $549$ as the product of the prime factors.
$549 = 3 \times 3 \times 61$
Write $387$ as the product of the prime factors.
$387 = 3 \times 3 \times 43$
H.C.F. will be the common factors of both the numbers.
Therefore, H.C.F. is $3 \times 3 = 9$
We know that the H.C.F. will be the length of the longest tile.
Therefore, the edge of the longest tile which will exactly fit is $9cm$.

Note:
We can evaluate the H.C.F. of the numbers by another method which is shown below:
Evaluate the H.C.F. by the long division method.
Divide the larger number by the smaller number and then divide the divisor by the remainder and continue this process until the remainder becomes $0$.
Hence, the final divisor on which remainder is $0$will be the H.C.F. of two numbers.

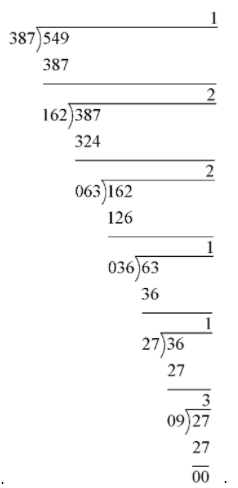
Hence, the H.C.F. of $549$ and $387$ is $9$.