Question

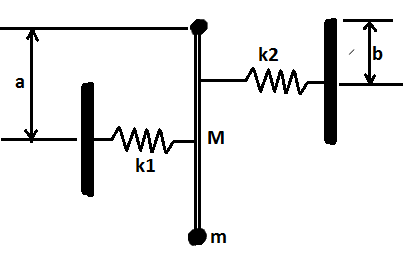
A rod of mass ${{M}}$ and length ${{L}}$ is hinged at its one end and carries a particle of mass ${{m}}$ at its lower end. A spring of force constant ${{{k}}_{{1}}}$ is installed at the distance ${{a}}$ from the hinge and another of force constant ${{{k}}_2}$ at a distance ${{b}}$as shown in the figure. The whole arrangement rests on a smooth horizontal table top. Find the frequency of vibration.

 

Answer 1

- Hint: Here in this combination we will experience an angular displacement due to the spring forces and because of that there will be a restoring force which will provide an inertia to the system. So, we will calculate all the above quantities and make a standard equation to get the value of the angular acceleration and with the help of that we will find the frequency of the system.

Complete step-by-step answer:
Here in this given problem we see that at point ${{A}}$ the rod is kept hinged.
Now we will do calculations for both the springs separately,
For spring which is at distance ${{b}}$,
Let us assume that the angular displacement of the rod from its mean position is ${{\theta }}$.
Now the extension for the spring connected at the distance ${{b}}$= ${{b\theta }}$
(Here angular displacement is so small that we have taken this as a linear displacement)
We can also calculate the restoring force for this spring ${{ = }}{{{F}}_{{b}}}{{ = }}{{{k}}_{{2}}}{{b\theta }}$
Moment of this force about point ${{A}}$=${{{I}}_{{b}}}{{ = }}{{{F}}_{{b}}}{{b}}$
${{{I}}_{{b}}}{{ = }}{{{k}}_{{2}}}{{b\theta }}{{.b}}$
${{{I}}_{{b}}}{{ = }}{{{k}}_{{2}}}{{{b}}^2}{{\theta }}$--equation (1)
For spring which is at distance ${{a}}$,
Similarly, the contraction for the spring connected at the distance ${{a}}$=${{a\theta }}$
(Here also angular displacement is so small that we have taken this as a linear displacement)
We can also calculate the restoring force for this spring ${{ = }}{{{F}}_{{a}}}{{ = }}{{{k}}_1}{{a\theta }}$
Moment of this force about point ${{A}}$is=${{{I}}_a}{{ = }}{{{F}}_a}{{b}}$
${{{I}}_a}{{ = }}{{{k}}_1}{{a\theta }}{{.a}}$
${{{I}}_a}{{ = }}{{{k}}_1}{{{a}}^2}{{\theta }}$--equation (1)
So total restoring force by both the springs =${{F = (}}{{{k}}_1}{{{a}}^2}{{ + }}{{{k}}_{{2}}}{{{b}}^2}){{\theta }}$
Now the total moment of inertia of the whole system about the hinged point ${{A}}$,
${{I = }}$moment of inertia about point A + moment of inertia of mass m about point A
${{I = }}\dfrac{{{{m}}{{{l}}^{{2}}}}}{{{3}}}{{ + m}}{{{l}}^{{2}}}{{ = }}{{{l}}^{{2}}}\left( {\dfrac{{{m}}}{{{3}}}{{ + m}}} \right){{ = }}\dfrac{{{{4m}}{{{l}}^{{2}}}}}{{{3}}}$-------equation (3)
So now for the calculation of the angular acceleration,
$\dfrac{{{{{d}}^{{2}}}{{\theta }}}}{{{{d}}{{{x}}^{{2}}}}}{{ = }}\dfrac{{{F}}}{{{I}}}{{ = }}\dfrac{{{{(}}{{{k}}_{{1}}}{{{a}}^{{2}}}{{ + }}{{{k}}_{{2}}}{{{b}}^{{2}}}{{)\theta }}}}{{\dfrac{{{{4m}}{{{l}}^{{2}}}}}{{{3}}}}}$
So here thus we have got an equation of type,
$\dfrac{{{{{d}}^{{2}}}{{\theta }}}}{{{{d}}{{{x}}^{{2}}}}}{{ + \omega \theta = 0}}$
So, on comparing this equation with the equation (4), we get
${{\omega = }}\sqrt {\dfrac{{{{(}}{{{k}}_{{1}}}{{{a}}^{{2}}}{{ + }}{{{k}}_{{2}}}{{{b}}^{{2}}}{{)}}}}{{\dfrac{{{{4m}}{{{l}}^{{2}}}}}{{{3}}}}}} $
And we know that frequency=${{f = }}\dfrac{{{\omega }}}{{{{2\pi }}}}$
Thus $f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{{{(}}{{{k}}_{{1}}}{{{a}}^{{2}}}{{ + }}{{{k}}_{{2}}}{{{b}}^{{2}}}{{)}}}}{{\dfrac{{{{4m}}{{{l}}^{{2}}}}}{{{3}}}}}} $

Note: Here from the relation of the angular frequency, ${{\omega }}$ and frequency, $f$ we can relate them for some more additional information. From the formula we can say that the angular frequency of any system or the object or particle is larger than the frequency by the factor ${{2\pi }}$.